Oh so many years ago I had my first insight into just how ridiculously confusing all the statistical terminology can be for novices.
I was TAing a two-semester applied statistics class for graduate students in biology. It started with basic hypothesis testing and went on through to multiple regression.
It was a cross-listed class, meaning there were a handful of courageous (or masochistic) undergrads in the class, and they were having trouble keeping up with the ambitious graduate-level pace.
I remember one day in particular. I was leading a discussion section when one of the poor undergrads was hopelessly lost. We were talking about the simple regression–a regression model with only one predictor variable. She was stuck on understanding the regression coefficient (beta) and the intercept.
In most textbooks, the regression slope coefficient is denoted by β1 and the intercept is denoted by β0. But in the one we were using (and I’ve seen this in others) the regression slope coefficient was denoted by β (beta), and the intercept was denoted by α (alpha). I guess the advantage of this is to not have to include subscripts.
It was only after repeated probing that I realized she was logically trying to fit what we were talking about into the concepts of alpha and beta that we had already taught her–Type I and Type II errors in hypothesis testing.
Entirely. Different. Concepts.
With the same names.
Once I realized the source of the misunderstanding, I was able to explain that we were using the same terminology for entirely different concepts.
But as it turns out, there are even more meanings of both alpha and beta in statistics. Here they all are:
Hypothesis testing
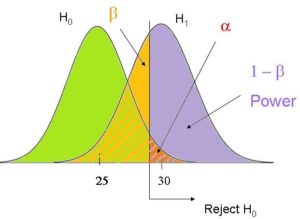
As I already mentioned, the definition most learners of statistics come to first for beta and alpha are about hypothesis testing.
α (Alpha) is the probability of Type I error in any hypothesis test–incorrectly rejecting the null hypothesis.
β (Beta) is the probability of Type II error in any hypothesis test–incorrectly failing to reject the null hypothesis. (1 – β is power).
Population Regression coefficients
In most textbooks and software packages, the population regression coefficients are denoted by β.
Like all population parameters, they are theoretical–we don’t know their true values. The regression coefficients we estimate from our sample are estimates of those parameter values. Most parameters are denoted with Greek letters and statistics with the corresponding Latin letters.
Most texts refer to the intercept as β0 (beta-naught) and every other regression coefficient as β1, β2, β3, etc. But as I already mentioned, some statistics texts will refer to the intercept as α, to distinguish it from the other coefficients.
Side note:
If the β has a ^ over it, it’s called beta-hat and is the sample estimate of the population parameter β. And to make that even more confusing, sometimes instead of beta-hat, those sample estimates are denoted B or b.
Standardized Regression Coefficient Estimates
But, for some reason, SPSS labels standardized regression coefficient estimates as Beta. Despite the fact that they are statistics–measured on the sample, not the population.
More confusion.
And I can’t verify this, but I vaguely recall that Systat uses the same term. If you have Systat and can verify or negate this claim, feel free to do so in the comments.
Cronbach’s alpha
Another, completely separate use of alpha is Cronbach’s alpha, aka Coefficient Alpha, which measures the reliability of a scale.
It’s a very useful little statistic, but should not be confused with either of the other uses of alpha.
Beta Distribution and Beta Regression
You may have also heard of Beta regression, which is a generalized linear model based on the beta distribution.
The beta distribution is another distribution in statistics, just like the normal, Poisson, or binomial distributions. There are dozens of distributions in statistics, but some are used and taught more than others, so you may not have heard of this one.
The beta distribution has nothing to do with any of the other uses of the term beta.
Other uses of Alpha and Beta
If you really start to get into higher level statistics, you’ll see alpha and beta used quite often as parameters in different distributions. I don’t know if they’re commonly used simply because everyone knows those Greek letters. But you’ll see them, for example, as parameters of a gamma distribution. Relatedly, you’ll see alpha as a parameter of a negative binomial distribution.
If you think of other uses of alpha or beta, please leave them in the comments.
See the full Series on Confusing Statistical Terms.
The first place I think the terminology drives my high school kids crazy is when we no longer write the equation of a line as y = mx + b like in algebra, but write it y = a + bx.
In algebra, b was the y-intercept. Now it’s slope. Geez, why do we do this to kids?
I really like the Hypothesis Testing graph. It’s one of the most comprehensive I’ve seen. Thank you for posting!
Thank you this is very helpful. I’m new to genomics and I get confused about alpha and beta when people talk about it. In genomics people use both regression and hypothesis testing frequently so I’m getting more confused and mixing up the betas. Now it’s clear to me after reading this post. Can you please talk about effect size and p-values as well?
kindly tell me if alpha+beta what will be answer
It’s a formulae…apha×beta =-b/a
Sorry…alpha+beta=-b/a
Hi, I am comparing stock returns on a monthly and daily basis, there are differences between the outcomes of the Hypothesis tests. Could you tell me a possible reason/s for the results?
Thanks
I have a confussion regarding the name and use of the product of dividing the estimator (coefficient) of a variable by its S.E.. In some places I found the called this Est./S.E. as standardized regression coefficient, is that right?
Thanks
hey, i was wondering if you can explain to me the assumptions that are needed for a and b to be unbiased estimates of Alpha and Beta. thanks ,
Thank you so much! You are very kind for spending your time to help others. Bless you and your family
hi, i am very new to stats and i am doing a multiple regression analysis in spss and two letters confuse me. The spss comes up with a B letter (capital) but here i see all of you talking about β (greek small letter), and when i listen to youtube videos i hear beta wades, what is their difference? Please help!!!!
calli,
its beta weight.. its a standarized regression coefficient [slope of a line in a regression equation]. it equals correlation when there is a single predictor.
Can you tell me why we use alpha?
wha is bifference between beta and beta hat and u and ui hat
Hi Ayesha, great question. The terms without hats are the population parameters. The terms with hats indicate the sample statistic, which estimates the population parameter.
but the population parameters are only theoretical, because we can’t get the entire data of nature and society to research? Is that so?
Correct.
Hi,
Im wondering about the use of “beta 0” In a null hypothesis.
What im wanting to test is “The effect of diameter on height = 0, or not equal to 0.
Having a lil trouble remembering the stat101 terminology.
I got the impression that that rather than writing:
Ho: Ed on H = 0
Ha: Ed on H ≠ 0
can I use the beta nought symbol like
B1 – B2 = 0 etc instead or am I way off track?
Hi Anna,
The effect of diameter on height is most likely the slope, not the intercept. It’s beta1 in this equation:
Height=beta0 + beta1*diameter
Here’s more info about the intercept: https://www.theanalysisfactor.com/interpreting-the-intercept-in-a-regression-model/
This is so helpful. Thx!!
I have read the Type I and Type II distinction about 20 times and still have been confused. I have created mnemonic devices, used visual imagery – the whole nine yards. I just read your description and it clicked. Easy peasy. Thanks!
Thanks, Carrie! Glad it was helpful.
Hi! This helps, but I am a little confused about this article I am reading. There is a table that lists the variables with Standardized Regression Coefficients. Two of the coefficients have ***. The *** has a note that says “alpha > 0.01”. What is alpha in this case? Is it the intercept? Is this note indicating that these variables are not significant because they are > 0.01? Damn statistics! Why can’t things be less confusing!?!?!
Hi Lyndsey,
That’s pretty strange. It’s pretty common to have *** next to coefficients that are significant, i.e. p < .01 (usually one * for < .05 and two ** for < .01). But they're saying "alpha >“, “not p <". And while yes, you want to compare p to alpha, that statement is no equivalent. I'd have to see it to really make sense of it. Can you give us a link?
I find SPSS’s use of beta for standardised coefficients tremendously annoying!
BTW a beta with a hat on is sometimes used to denote the sample estimate of the population parameter. But mathematicians tend to use any greek letters they feel like using! The trick for maintaining sanity is always to introduce what symbols denote.
Ah, yes! Beta hats. This is actually “standard” statistical notation. The sample estimate of any population parameter puts a hat on the parameter. So if beta is the parameter, beta hat is the estimate of that parameter value.