One of Stata’s incredibly useful abilities is to temporarily store calculations from commands.
Why is this so useful?
Let’s start with an illustrative example: centering predictors.
Let’s say I’m trying to explain how important a college education is to my kids. So I decide to be scientific and load a data set of wage information into Stata. To make it simple for the kids I decide not to control for variables such as gender and race (I save that for a later discussion).
So I decide to regress years of education on salary. Here are my results:
Looking at my results I tell my kids that for every year of education their annual salary will increase by $3,910.
They sound excited and look at my table and ask “who is “_cons” and why does that person make a negative $18,331?” I explain that is the constant or y-intercept. That is your starting point. Everyone is going to start out earning a negative $18,331.
Say What? Now they are really confused because I did a horrible job of explaining this.
Let me try this again. What I should have done was found the mean for the number of years of education in my data set. I then create a new variable “educ_mean” which has centered education at the mean (the mean of “educ_mean” is zero).
To find the mean I run the summary command for “educ”.
To create the new variable, educ_mean, I subtract the mean of the educ from educ.
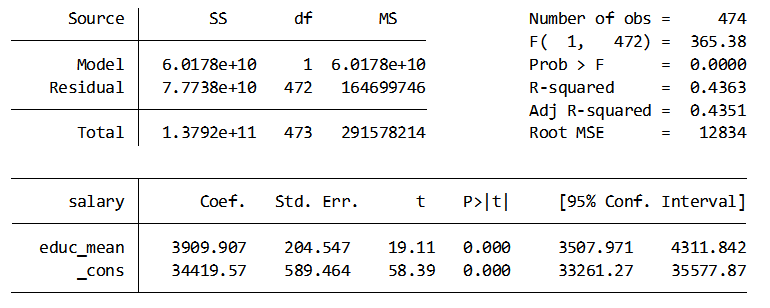
I then run the regression using the mean-centered variable.
So now I explain to my kids that the average person has 13 ½ years of education. On average that person can expect to earn $34,419.57.
For every year greater than 13 ½ years of education you can expect to make $3,909.91 more per year.
For every year less than 13 ½ years of education you can expect to make $3,909.91 less per year.
Now they understand and are doing a cost benefit calculation to determine whether it pays to go to college.
Stata and stored calculations
I could create this centered variable by simply subtracting 13.49146 from my original education variable. But what if I need to center numerous variables? How many decimal places should I include in my calculations to have accurate results? How can I reduce my time running data and increase my accuracy?
Using Stata’s stored calculations reduces input errors and improves accuracies. The calculations from most of Stata’s general commands and all of its estimation commands are temporarily stored for your use.
So instead of a two-step process where I calculate the mean, then subtract the answer from my education variable, I can simply ask Stata to subtract it’s stored mean value from the education variable.
Examples of general commands that store results are: summarize, pairwise correlation (pwcorr), and confidence intervals (ci). Examples of estimation commands are: regress, mixed, and logit.
Besides storing calculations (known as scalars in Stata speak), Stata also stores words (called macros) and tables (matrices).
To view the stored data after a general command you type “return list”. To view the stored data after running an estimation command you type “ereturn list”.
The stored information for the summary of educ as well as the stored data generated after running the regression is shown below.
The code for creating the new variable using the stored data is:
sum educ
gen educ_mean=educ-r(mean)
Additional note: Easy way to standardize a variable
The stored result from the summary of a variable contains the standard deviation as well as the means. To standardize educ I simply subtract r(means) from educ and then divide by r(sd).
sum educ
gen educ_std=(educ-r(mean))/r(sd)
Jeff Meyer is a statistical consultant with The Analysis Factor, a stats mentor for Statistically Speaking membership, and a workshop instructor. Read more about Jeff here.


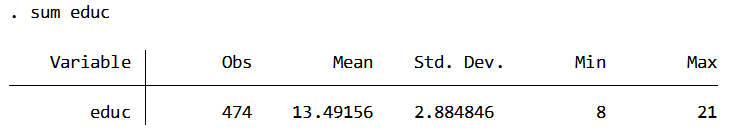

Very well explained. Just one question- when does one decide to use the centred predictors in the model instead of actual predictor values?
Thanks
Meenu
Thanks Meenu,
There are at least two primary reasons to center predictors (and possibly more). One is to reduce the possibility of multicollinearity, especially when introducing quadratic predictors to your model. The second reason, which is used most often, is to improve interpretability of the model. Centering a predictor has no impact on the results of the model. Your coefficients won’t change but the value of the constant will.
Here are links to two articles that Karen wrote on the subject:
https://www.theanalysisfactor.com/centering-for-multicollinearity-between-main-effects-and-interaction-terms/
https://www.theanalysisfactor.com/glm-in-spss-centering-a-covariate-to-improve-interpretability/
Thanks for your questions,
Jeff
Awesome. Thanks very much Jeff.
Meenu