When you hear about multilevel models or mixed models, you very often think of a nested design. Level 1 units  nested in Level 2 units, which are in turn possibly nested in Level 3 units. But these variables that define the units and that become random factors in the model can, in fact, be crossed with each other, not nested.
nested in Level 2 units, which are in turn possibly nested in Level 3 units. But these variables that define the units and that become random factors in the model can, in fact, be crossed with each other, not nested.
Mixed models with crossed random factors are a little trickier to wrap your head around than mixed models with nested random factors. They still involve some nesting. But they’re not harder to analyze and they are quite common in many fields. Recognizing when you have one and knowing how to analyze the data when you do are important statistical skills.
The Nested Multilevel Design
Let’s start by reviewing the more common design: nested. The most straightforward use of Mixed Models is when observations are clustered or nested in some higher group.
It’s also so common that it often has its own name: multilevel model.
Examples include studies where patients share the same doctor, plants grow in the same field, or participants respond to multiple experimental conditions.
The units of observation at Level 1 (patient, plant, response) are clustered at Level 2 (doctor, field, or participant). This makes the responses from the same cluster correlated.
In these models, the Level 2 cluster is not something you’re interested in testing hypotheses about. It’s what we call a “blocking factor.” Even so, you need to control for its effects.
If the researcher would like to generalize the results to all doctors, fields, or participants, these clustering variables are random factors. You account for and measure its effects through random intercepts and/or adding random slopes across this factor for any level 1 predictor.
The observations of the dependent variable are always measured on the Level 1 unit (the patient, plant, or time point). Predictor variables (fixed effects) can be measured at either Level 1 or Level 2. For example, number of years of experience of a doctor would be at Level 2, measured for each doctor. But patient age would be measured at Level 1, measured for each patient.
You assume the values of the response variable within cluster are are correlated, but the observations between clusters are independent.
A third level (or more) is possible as well. This would happen if each doctor sees all their patients at one of four hospitals or each field has only one of 5 species.
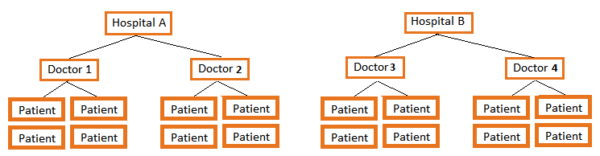
The Crossed Multilevel Design
In one kind of 2-level design, there is not one random factor at Level 2, but two crossed factors. Each is a different random factor and they’re crossed with each other.
Each observation at Level 1 is nested in the combination of these two random factors. These models need to be specified correctly to capture the effects of both random factors at Level 2.
Here are the same examples with crossed random factors:
Example 1:
Every patient (Level 1) sees their Doctor (Random Factor at Level 2) at one of four Hospitals (Random Factor at Level 2) for a study comparing a new drug treatment for diabetes to an old one.
Each doctor sees patients at each of the hospitals. That means Hospital and Doctor are crossed. (If each doctor worked at only one hospital, doctor would be nested within Hospital). Patient responses vary across doctors and hospitals.
Because each Patient sees a single doctor at a single hospital, patients are nested in the combination of Doctor and Hospital.
The response is measured at Level 1–the patient. Predictors can occur at Level 1 (age, diet) or either Level 2 factor (years of practice by doctor, size of hospital).

The analysis would need to include, at a minimum, a random intercept for Doctor and a random intercept for Hospital.
Example 2:
An agricultural study is studying plants in 6 fields.
While there are many species of plants in each field, the researcher randomly chooses 5 species to be in the study. Each of the 5 species is found in every field.
Each individual plant (Level 1 unit) grows within one combination of species and field. Since every species is in every field, Species and Field are crossed at Level 2.
The response (nitrogen uptake) is measured at Level 1–the plant. Predictors can occur at Level 1 (height of plant) or either Level 2 factor (type of fertilizers applied to the field, whether the species is native or introduced).
Example 3:
In a social psychology experiment on first impressions, subjects rate statements that describe behaviors done by a fictional person, Bob.
On each trial, subjects rate whether or not they find Bob’s behavior friendly. The response time of the rating is recorded. Trial is the Level 1 unit.
Each subject sees the same 10 friendly and 10 unfriendly behaviors. The behaviors are not in themselves of interest to the experimenter, but are representative of all friendly and unfriendly behaviors that Bob could perform.
Because responses to the same behavior tend to be similar, it is necessary to control for their effects. After all, even within friendly behaviors, some (giving a gift) may be generally rated more friendly than others (holding a door open). Each trial of the experiment (Level 1) is nested within the combination of Subject and Behavior, which are both random factors at Level 2.
Subject and Behavior are crossed at Level 2 since every Subject rates every Behavior. The response is measured at Level 1–the trial. Predictors can occur at Level 1 (a distractor occurs on some trials) or either Level 2 factor (Behavior is friendly or not, Subject is put into positive, neutral, or negative mood).
Analysis issues
Luckily, standard mixed modeling procedures such as SAS Proc Mixed, SPSS Mixed, Stat’s mixed, or R’s lmer can all easily run a mixed model with crossed effects model. (R’s lme can’t do it).
However, I’ve also seen issues with software that is designed specifically for Multilevel (aka Nested) designs. It assumes that all random factors are nested within each other. For example, a member was once trying to use a software designed for estimating sample sizes in multilevel models. It would only allow one random factor at level 2. So that software just didn’t work for that design.
At a minimum, each random factor needs a random intercept. The random factor itself is defined as the “subject” in the random part of the mixed model. You need two. You don’t need to specify to the software that the two random factors are crossed. With the data in long format, your software can tell.
Where it gets tricky is when deciding which random slopes you can include in the model. Each random factor can potentially have random slopes in addition to random intercepts. But this depends on the specific design of the study.
And of course, a study design can get even more complex. You could have more than the two random factors than we’ve talked about here. And they can be crossed or nested with each other.
Updated 10/2023


Why does your example say 4 hospitals in the description, but the graphic visual depicting it shows only hospital A and hospital B?
Just to make the picture fit. 🙂
Gaining understanding of ‘The Crossed Multilevel Design’ will help me in my teaching and research. Thanks
This summary discussion of very interesting and useful to enhance the clear understanding between the two concepts.
Hi,
Thanks for this interesting thread. In example 2, if we had a case in which not every species was in every field, rather it was be partially nested and partially crossed, what would be the case? would you still consider this as crossed at level 2?
That’s a great question. There are definitely situations where neither crossed or nested is entirely true. You can call it partially crossed. Ultimately, you can try to fit an interaction and it may or may not run. Just try it.
Hi Karen,
I am doing an experiment where I have four groups of individuals, which are exposed to different temperatures:
Group 1 (12 individuals): week 1 to 4: ambient (control group)
Group 2 (12 individuals): week 1: ambient, week 2-4: +2C
Group 3 (12 individuals): week 1: ambient, week 2: +2C, week 3-4: +4C
Group 4 (12 individuals): week 1: ambient temperature week 2: +2C week 3: +4C, week 4: +6C.
I want to look at the effect of temperature on various continuous behavioural responses at the level of the four different temperatures not taking into account groups, but also at the group/individual level, i.e. taking into consideration the repeated measurements and the different temperatures the individuals are exposed to with each repeated measure.
Is a multi-level model with crossed random effects suitable for this question?
Thanks,
Beth
Hi Beth,
I really can’t give advice without asking you a lot of questions. We do have consulting services and a membership if you need advice and want to talk with someone.
Dear Karen,
I have a question related to the third example, which (I think) is similar to the experiment I did. Unfortunately, I do not know how to specify the model because I cannot find any literature related to this kind of multilevel application, as in most applications in the literature, individuals are nested in classes etc.
I tried to specify the model in MPLUS but their support told me ‘you have no multilevel situation’.
Now I found your example, which seems quite similar, so I still have hope that I am not totally wrong.
In my experiment, each participant was exposed to the same 25 stimuli that reflect five different categories of theoretical interest (5 stimuli representing each category). Hypotheses are concerned with differences between the five categories. To control for variances caused by differences in the stimuli representing each category, I aimed to use a multilevel approach. Dependent variables are a continuous response-time measure and a binary coded answer.
Is it correct that in my case trials are nested in the five categories as well as the individuals? Or is it that trials are nested in the individuals as well as in the 25 stimuli that are nested in the five categories?
Maybe you are aware of similar applications in literature and/or text books?
Thank you very much for your help!
Daniel
Hi Daniel,
Yes, these are tricky. I don’t know for sure whether MPlus can do them as your random factors are not nested into different “levels.” They’re crossed. Trials are nested in the individual*category interaction. Individuals are crossed with both stimulus and category. Stimuli are nested in category.
If you think of this as a mixed model instead of multilevel, it will be easier. Think of each variable as fixed or random.
How can I download this
Hi Karen,
Do you have example code for your first example in SAS that you can share. How would I code for controlling for both patient and physician characteristics on one model?
Thanks for the help!
Is this the same as a cross-level interaction for a multilevel model?
Hi Patricia,
It’s not. A cross-level interaction in a multilevel model is an interaction among fixed effects, one of which is measured at level 1 and one of which is at level 2. The fact that you have level 1 and 2 indicates the random effects are nested. For example: students nested within teachers because each student has only one teacher.
Crossed random effects means that your random factors themselves are crossed, not nested. So not each student having one teacher. Each student having every teacher.
Hi Karen!
First thank you, because this is the first article that gives me a clue, that what I have is called as “crossed design” in some way.
But it seems, that I have a doubled crossed design:
I got participants that reacted to 6 different alarms in 2 different alarm conditions. Every participant did the 6 alarms in both conditions (the order of condition was randomized, but it does not have an effect at the particular dependent variable).
My problem is, that one of my dependent variables is nominal: they should identify the alarm and this variable has the values “identified correctly” and “identified wrong”.
So with all other variables (on ratio scale) I just take the mean over the 6 alarms and use a repeated-measure ANOVA (hopefully this is correct, as the variance between alarms is small and the number is equal). But with this dichotomous variable I cannot just take the mean, am I right? So that I have to look at the alarms as another level in multilevel modeling?
Do you have a clue what to do or am I just thinking wrong?
Thanks a lot in advance!
Hi Eva,
Yes, you’ve got a mixed model. I would also not average 6 responses on the numerical outcomes. When you do that, you’re ignoring variability.
Mixed designs can get complicated fast.
Hi Karen!
Thanks, as always your explanation are very paedagogic!
A question: can you introduce a fixed effect, an independent variable, at the intersection of your two random effects at level 2? For instance, in your first example, if Dr A is happier at hospital 1 than at hospital 2; or if each doctor’s office differs by hospital? Or would you have to introduce a new level 2, say, doctors’ office, or a “doctor by hospital” level, which then is cross-classified by a doctors and hospitals (now being level 3)?
Thanks again!
Best wishes/Klara
Hi Klara,
Yes, you can. The doctor*hospital interaction exists as a “unit of measurement.”
Hi Karen,
Thanks so much for this very helpful page. I have a question for you if you have the time: Is there any minimum requirement for the number of observations within each cross-classification (each cell, if you’re thinking of it in terms of rows-by-columns)? Without getting into the details, I have a study in which “Raters” evaluated stimuli collected from “Donors” (and nearly every Rater evaluated stimuli from each of the Donors). Thus, stimulus ratings are cross-classifed into Rater-by-Donor cells. I plan to examine how these ratings vary as a function of Rater characteristics, Donor characteristics, and the compatibility of each Rater-Donor pair (specifically, proportion of alleles that the Rater and Donor have in common at one particular locus). So, a cross-classified model seems like the way to go. The only potential problem is that each cell will contain just one single rating… or is that not a problem? Thanks!
Hi Kelly,
One is sufficient. It means there will be some interactions you can’t test, but this is a very common design.
Hello,
My data contains product prices, observed for several stores, which belong to a particular chain.
I’m thinking of doing a variance decomposition. Thing is I’m not sure how my model should look like. I should have a Random Effect for chain, and for store. But how about products?
Thank you in advance for any suggestion.
Hi Joaquin,
It could be that chain, store, and product are all random factors or just some. I would have to know much more detail about your study.
How about this example–-does it apply? I study a personality trait that can be inferred from videos. The trait differs by sexual orientation (gay/straight). I have 60 targets (30 gay 30 straight) and 60 raters (30 gay and 30 straight; we are interested in whether rater’s sexual orientation increases accuracy). We’d like to generalize both beyond our targets and beyond our raters, so in that sense we’d like to consider them random effects. Every rater sees every target, so this seems completely crossed. I’m having trouble mapping my situation onto any of the above though.
Hi Mike,
It’s honestly hard for me to tell without really understanding every detail of the design, but it certainly sounds like it applies. Your raters are technically your “subjects” and the targets are like the “trials.”
Hi Karen —
Thank you so much for your site — it is an amazing resource, and has helped clarify my thinking about these issues a lot. I am also writing to ask about your example 3 above. In that scenario, I read distractor as being nested within both participant and behavior — as some participants may be more sensitive to distractors than others and some behaviors may be more or less prone to disruption by distractors. When modeling this in SPSS, is the idea that distractor would be added as a fixed effect, and then nested within the two random effect commands?
Many thanks,
Emily
I’m not sure what you mean by conditions or replicates. We do not have treatment groups. All images were viewed by all subjects in the study and the response is measured at the image level. I want to examine the effect of different demographic factors on the response. I also want to include whether the image was viewed first in the model. Do I have to do anything special when specifying the model if some covariates measured at the image level and others at the subject level?
I have a study that I think has crossed random effects. Participants rated 7 images on the same outcome variable. Each participant rated the same 7 images (in random order). Dependent variables are demographics and some other variables measured at the image level. I’m wondering how do you specify this with SAS? Do I do two random statements?
Also, my original thought with how to analyse this data was to use a random intercept model. Then I could include image as a covariate to see the differences in ratings for each image. Would that be valid?
Hi Sarah,
It could be. It depends on whether those 7 images represent 7 conditions or if some are replicates. If you want to compare the actual images, then don’t make it random.
But yes, two random statements in SAS. You can have a random intercept for subject and a random intercept for image.
Thanks so much for discussing this topic, I am having a hard time understanding the differences between nesting and cross-classification and this post definitely points me in the right direction!
I am trying to understand the difference between the two with respect to a standard repeated measures design (for example, measuring participants’ emotional responses to a stressor for 1 hour at 10 minute intervals). I am used to thinking of this type of design as time nested within participant, but now I am wondering if time and participant are actually crossed because each participant is measured at every time (and every time is assessed for every participant). Am I understanding this correctly?
1) IF NO: can please you elaborate on the difference between nested and cross-classified designs? I must have misunderstood something along the way.
2) IF YES: I am unclear why ‘trial’ in your third example is nested within behavior and participant. Doesn’t every participant receive every trial just like every participant receives every behavior? I am not clear as to why this design is not completely cross-classified.
Also, do you know of any resources for SPSS nested versus cross-classified syntax?
Thank you for your help!
Hi Lisa,
Great questions.
In answer to your first question, you are correct–in a standard repeated measures study where every participant is measured at every time point, participant and time point are crossed.
2) Trial, in this example, is literally the individual trial, not the behavior. If 15 subjects each see 10 behaviors, that’s 150 trials. Each of those trials occurs for only one subject and one behavior. So each subject has 10 trials. So subject and behavior are crossed, but trail is nested within both subject and trial.
Make sense?
Karen
Thanks for your quick and helpful response! I am still slightly confused. I hate to get hung up on a specific example, but this example is very relevant to my own research, so figuring out the source of my confusion will go a long way!
I think I am unclear about why we need to define ‘trial’ and how we would use ‘trial’ in an analysis. Specifically, it sounds like trial is just a combination of subject and behavior such that each trial is a unique combination of one person and one behavior. If that is the case, why do we need to identify trial in addition to subject and behavior – doesn’t specifying subject and behavior give us this information already?
I am not sure if the following metaphor will make sense, but it feels similar to specifying a particular ‘cell’ in a factorial experiment. If there are two independent variables with two levels each, there are four total ‘cells’. These cells are a combination of the other two factors and they are unique. I guess I am confused because I don’t understand why we need to define the specific ‘cell’ because (at least in an anova framework) those cells are created automatically by defining two crossed factors.
Is there any chance you have SPSS syntax written for example 3? Perhaps seeing the actual syntax will help me figure things out. Thanks again for your help!