The linear model normality assumption, along with constant variance assumption, is quite robust to departures. That means that even if the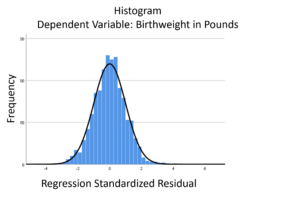 
assumptions aren’t met perfectly, the resulting p-values and confidence intervals will still be reasonable estimates.
This is great because it gives you a bit of leeway to run linear models, which are intuitive and (relatively) straightforward. This is true for both linear regression and ANOVA.
You do need to check the assumptions anyway, though. You can’t just claim robustness and not check. Why? Because some departures are so far off that the p-values and confidence intervals become inaccurate. And in many cases there are remedial measures you can take to turn non-normal residuals into normal ones.
But sometimes you can’t.
Sometimes it’s because the dependent variable just isn’t appropriate for a linear model. The (more…)
There are not a lot of statistical methods designed just to analyze ordinal variables.
But that doesn’t mean that you’re stuck with few options. There are more than you’d think.
Some are better than others, but it depends on the situation and research questions.
Here are five options when your dependent variable is ordinal.
(more…)
What do you do if the assumptions of linear models are violated?
(more…)
Interactions in statistical models are never especially easy to interpret. Throw in non-normal outcome variables and non-linear prediction functions and they become even more difficult to understand. (more…)
Interpreting the Intercept in a regression model isn’t always as straightforward as it looks.
Here’s the definition: the intercept (often labeled the constant) is the expected value of Y when all X=0. But that definition isn’t always helpful. So what does it really mean?
Regression with One Predictor X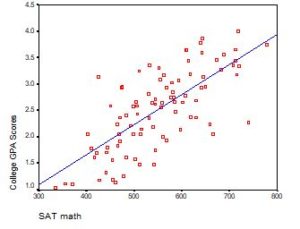
Start with a very simple regression equation, with one predictor, X.
If X sometimes equals 0, the intercept is simply the expected value of Y at that value. In other words, it’s the mean of Y at one value of X. That’s meaningful.
If X never equals 0, then the intercept has no intrinsic meaning. You literally can’t interpret it. That’s actually fine, though. You still need that intercept to give you unbiased estimates of the slope and to calculate accurate predicted values. So while the intercept has a purpose, it’s not meaningful.
Both these scenarios are common in real data. (more…)
Multinomial logistic regression is an important type of categorical data analysis. Specifically, it’s used when your response variable is nominal: more than two categories and not ordered.
(more…)
assumptions aren’t met perfectly, the resulting p-values and confidence intervals will still be reasonable estimates.
