Interpreting the Intercept in a regression model isn’t always as straightforward as it looks.
Here’s the definition: the intercept (often labeled the constant) is the expected value of Y when all X=0. But that definition isn’t always helpful. So what does it really mean?
Regression with One Predictor X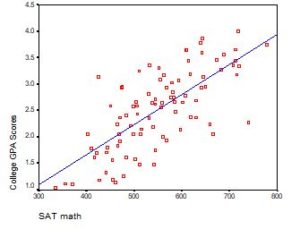
Start with a very simple regression equation, with one predictor, X.
If X sometimes equals 0, the intercept is simply the expected value of Y at that value. In other words, it’s the mean of Y at one value of X. That’s meaningful.
If X never equals 0, then the intercept has no intrinsic meaning. You literally can’t interpret it. That’s actually fine, though. You still need that intercept to give you unbiased estimates of the slope and to calculate accurate predicted values. So while the intercept has a purpose, it’s not meaningful.
Both these scenarios are common in real data.In scientific research, the purpose of a regression model is one of two things.
One is to understand the relationship between predictors and the response. If so, and if X never = 0, there is no interest in the intercept. It doesn’t tell you anything about the relationship between X and Y.
So whether the value of the intercept is meaningful or not, many times you’re just not interested in it. It’s not answering an actual research question.
The other purpose is prediction. You do need the intercept to calculate predicted values. In market research or data science, there is usually more interest in prediction, so the intercept is more important here.
When A Meaningful Intercept is Important
When X never equals 0, but you want a meaningful intercept, it’s not hard to adjust things to get a meaningful intercept. Simply consider centering X.
Centering sounds fancy, but it’s not. It means to re-scale X so that the mean or some other meaningful value = 0. And all you do to get that is create a new version of X where you just subtract a  constant from X. Let’s say X is Age and the mean of Age in your sample 20.
constant from X. Let’s say X is Age and the mean of Age in your sample 20.
It will look something like: NewX = X – 20.
That’s it.
Just use NewX in your model instead of X. Now the intercept has a meaning. It’s the mean value of Y at the mean value of X.
Interpreting the Intercept in Regression Models with Multiple Xs
It all gets a little trickier when you have more than one X.
The definition still holds: the intercept is the expected value of Y when all X=0.
The emphasis here is on ALL.
And this is where it gets complicated. If all Xs are numerical, it’s an uncommon (though not unheard of) situation for every X to have values of 0. This is often why you’ll hear that intercepts aren’t important or worth interpreting.
But you always have the option to center all numerical Xs to get a meaningful intercept.
And when some Xs are categorical, the situation is different. Most of the time, categorical variables are dummy coded. Dummy coded variables have values of 0 for the reference group and 1 for the comparison group. Since the intercept is the expected value of Y when X=0, it is the mean value only for the reference group (when all other X=0). So having dummy-coded categorical variables in your model can give the intercept more meaning.
This is especially important to consider when the dummy coded predictor is included in an interaction term. Say for example that X1 is a continuous variable centered at its mean. X2 is a dummy coded predictor, and the model contains an interaction term for X1*X2.
The B value for the intercept is the mean value of X1 only for the reference group. The mean value of X1 for the comparison group is the intercept plus the coefficient for X2.
It’s hard to give an example because it really depends on how X1 and X2 are coded. So I put together six situations in this follow up article: How to Interpret the Intercept in 6 Linear Regression Examples


Dear Madam Karen,
Thanks a lot and well received
Plea how can I interpret this regression equation with a negative intercept? Y=-2.73+5.4x? I come across a negative intercept of a regression model
There’s really no difference in interpreting a negative intercept, unless negative values aren’t possible for that variable. Not every intercept has a meaningful interpretation.
Hello, i have a question for my test that i hope i will find the answer here.
I made a calibration curve for my toxine with 6 differents concentration (in ng/mL) and i got a R2= 0.99 and y=10.273x – 20.395.
Is it logic that the accuracy of intercept is higher than that of the slope ? and why this happened!
thank you and what am i doing now?
Thanks so much for your explanations, Karen! I have a question: can I interpret the intercept (Y) in a regression model where my intercept is significant and two other predictors ( say X and Z), while X can never be zero but Z can be 0 ?
In my case Y is a change score. If the intercept is not equal to zero and significant can I infer from this that there is an overall change?
Hi Alina,
The intercept is only interpretable if all predictors (X and Z) can be zero.
Hi, I m analyzing logistic regression for my independent and dependent variables, form the regression coefficient I want to calculate risk score of the independent variables on dependent variable. but in the regression model i got few variables have significant association and others have no significant relation with my dependent variables. so when calculating my score should I consider the intercept of the model with all significant and non significant independent variables or I should analyse another logistic regression with only the independent variables those are significant and then should take that intercept value ? please guide me….
thanks
this is useful
Hi, pls answer me,
Can intercept be zero In regression analysis??
Sure. You just don’t want to force it to be.
Thank you Karen for this answer
Please I would like to ask about LOD using a regression calibration line. Is it more beneficial to put x=0 and y=0 or not? Knowing that I do not tried this in lab but the variables are really related theoretically so that at x=0 y also must be equal 0. And when I do this the regression equation contains a value for the intercept although I have put it 0. Can I understand why? And is this true to put intercept 0 at x=0 when calculating LOD??
yes
Hi Karen,
I’m using my model to calculate predicted values so I need to include the constant. I’m concerned however that whilst my 3 regression variables are significant, the constant is not. I’m concerned that the constant being not significant means that I can’t be confident about the predicted values.
Thoughts?
Thanks
John
Hi John,
The p-value for the constant isn’t important. It’s testing the null hypothesis that the constant = 0.
So even if the constant isn’t significantly different from 0, including it will still give you more accurate predicted values AND more accurate slopes than if you eliminate it. When you eliminate it, you set it to 0.
Thanks Karen!
Everything is very open with a clear explanation of the issues.
It was really informative. Your site is very helpful.
Many thanks for sharing!
Thank you for this. May I suggest that it may be really helpful to use an example with real data to help explain how this works? For me (and I expect for others too), it would make it much easier to understand.
I 100% agree. YES
Why value of intercept is zero?
If intercept is not in the model than what happened?
Is this is possible??the intercept term of a regression model is negative??Can u make me clear with an easy example plz???
Case Summaries
Imp
Type N Mean
1 7 5.86
2 4 5.75
3 89 4.61
Total 100 4.74
How to interpret the above? 1 = Manufacturer; 2 = Distributor; 3 = Retailer of a product.
RECODE Type (1=0) (2=0) (3=1) INTO retail.
EXECUTE.
REGRESSION
/MISSING LISTWISE
/STATISTICS COEFF OUTS R ANOVA
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT Imp
/METHOD=ENTER Size retail.
How to interpret the above? 1 = Manufacturer; 2 = Distributor; 3 = Retailer of a product
Anil Bandyopadhyay
Can we use negstive intercept ?
I have two nagative intercept what can i do
Yes, intercepts can be negative even if Y can’t. This usually occurs when none of the X values are close to 0.
what if coefficient of regression is 1.797?
why intercept used negative any way??????????
what happend if the intersept in not in minus. i m confuse i found some are in positive and some are in negative intesept..
please clarify.
Hi,
What if you use a tobit model where the dependent variable takes values of zero or more than zero and you get a negative intercept. You run the tobit model and you observe a negative constant. What does this mean in this case?
What is the fixed and estimated value in regression equation? a or b?
Please reply asap .☺
Wow. Thanks so helpful
Does the value of the intercept ever change, for example, when you are trying to interpret significant interaction terms? Say, I have three predictors, X1, X2, and X3 in a significant interaction. X1 is a four level categorical, and the other two are centered and continuous. So, the intercept can be defined as one level of X1, X2 = mean, and X3 = mean. And I can see that there is a 3-way interaction in which for one level of X1 (relative to the intercept as defined above), as X2 goes up and X3 goes up by one unit, I need to adjust the estimate for the simple effect of that level of X1 by some amount. But I am confused how this then relates back to the intercept. Is it really still defined as above? Or once I start considering the interaction, do I also change the designation for X2 and X3 in the intercept? Thanks.
What if you intercept isn’t significant, and you are using a dummy variable? Should you still use it in your prediction equation?
Thanks!
Yes. 🙂
I have regression equation y=74.626+1.2x, then how can the meaning of y-intercept be interpreted?
Why would you use the intercept even tough it is not significant?
Are there any citable sources to use the intercept, even tough it is insignificant?
Thanks
I will like to ask, when dealing with two indepents variable and our priori expectation for our coefficient is said to be greater than zero, what of if it happens that the intercept is negative, are we saying this is significant or insignificant ?
If I built 3 index variables and several dummy variables, then was told to test to see if there is a relationship between how satisfied employees are in their job (index variable 1) and how they see the environment around them. I ran the regression and my results were that my two Independent Variable Indexes were significant, but my constant was not. The Adj. R-square was .608 and the F Sig was .000.
What am I doing wrong?? Or what can I interpret from my results?
In a negative binomial regression, what would it mean if the Exp(B) value for the intercept falls below the lower limit of the 95% Confidence Interval?
Hmm, not sure I understand your question. CI for what?
Hi! What happens if all of my variables can be 0 which had a significant regressions coefficient? (I have four Xs, 3 of them have a significant coefficient and can be 0 as they are either dummies or are on a scale from 0 and there are 0s in the sample, but one of the Xs cannot be 0. It’s also the one with not significant coefficient.)
Thanks!
Hi Irena,
If ANY of the Xs can’t be 0, then the intercept doesn’t mean anything. Or rather, it’s just an anchor point, but it’s not directly interpretable.
als would like to as about, if we decrease sample by half will SSE, SSR, SST increase or decrease, a bit confused.
None would change, theoretically. Sums of Squares are not directly affected by sample size.
does this mean that if education is =to zero, i.e no education, then the expected mean of y =-5
Yes.
quetion: if wage =-5+10*years of education and wage is measure in 1000s; how do you interpret the coeffficient and does the intercept make sende
This sounds like a homework question, so I’m going to try to answer only by getting you to think through it.
Since the intercept ALWAYS is the mean of Y (1000 of dollars or whatever the currency is) when X=0, it will only be meaningful if it’s meaningful that X=0 AND if there are examples in the data set. Is there anyone in the data set with years of education = 0?
I’d like to now why the need for a column of ones in the model to account for the intercept. I would need a basic answer, since I’m not a mathematician. Thank you.
In the X matrix, each column is the value of the X that is multiplied by that regression coefficient.
Since the intercept isn’t multiplied by any values of X, we put in 1s.
It makes all the matrix algebra work out.
Karen