
In the world of statistical analyses, there are many tests and methods that for categorical data. Many become extremely complex, especially as the number of variables increases. But sometimes we need an analysis for only one or two categorical variables at a time. When that is the case, one of these seven fundamental tests may come in handy.
These tests apply to nominal data (categories with no order to them) and a few can apply to other types of data as well. They allow us to test for goodness of fit, independence, or homogeneity—and yes, we will discuss the difference! Whether these tests are new to you, or you need a good refresher, this training will help you understand how they work and when each is appropriate to use.
(more…)
One question that seems to come up pretty often is:
What is the difference between logistic and probit regression?
Well, let’s start with how they’re the same:
Both are types of generalized linear models. This means they have this form:
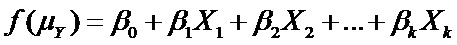
(more…)
There are not a lot of statistical methods designed just for ordinal variables.
But that doesn’t mean that you’re stuck with few options. There are more than you’d think. (more…)
Like the chicken and the egg, there’s a question about which comes first: run a model or test assumptions? Unlike the chickens’, the model’s question has an easy answer.
There are two types of assumptions in a statistical model. Some are distributional assumptions about the residuals. Examples include independence, normality, and constant variance in a linear model.
Others are about the form of the model. They include linearity and (more…)
The assumptions of normality and constant variance in a linear model (both OLS regression and ANOVA) are quite robust to departures. That means that even if the assumptions aren’t met perfectly, the resulting p-values will still be reasonable estimates.
But you need to check the assumptions anyway, because some departures are so far off that the p-values become inaccurate. And in many cases there are remedial measures you can take to turn non-normal residuals into normal ones.
But sometimes you can’t.
Sometimes it’s because the dependent variable just isn’t appropriate for a linear model. The (more…)


