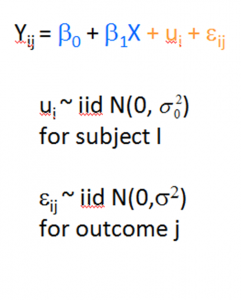I recently received a great question in a comment about whether the assumptions of normality, constant variance, and independence in linear models are about the errors, εi, or the response variable, Yi.
The asker had a situation where Y, the response, was not normally distributed, but the residuals were.
Quick Answer: It’s just the errors.
In fact, if you look at any (good) statistics textbook on linear models, you’ll see below the model, stating the assumptions: (more…)
If you have run mixed models much at all, you have undoubtedly been haunted by some version of this very obtuse warning: “The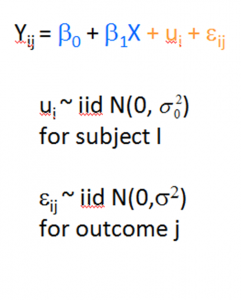 
Hessian (or G or D) Matrix is not positive definite. Convergence has stopped.”
Or “The Model has not Converged. Parameter Estimates from the last iteration are displayed.”
Let’s start with some background. If you’ve never taken matrix algebra, (more…)
One issue in data analysis that feels like it should be obvious, but often isn’t, is setting up your data.
The kinds of issues involved include:
Answering these practical questions is one of those skills that comes with experience, especially in complicated data sets.
Even so, it’s extremely important. If the data isn’t set up right, the software won’t be able to run any of your analyses.
And in many data situations, you will need to set up the data different ways for different parts of the analyses. (more…)
One of the most difficult steps in calculating sample size estimates is determining the smallest scientifically meaningful effect size.
Here’s the logic:
The power of every significance test is based on four things: the alpha level, the size of the effect, the amount of variation in the data, and the sample size.
You will measure the effect size in question differently, depending on which statistical test you’re performing. It could be a mean difference, a difference in proportions, a correlation, regression slope, odds ratio, etc.
When you’re planning a study and estimating the sample size needed for (more…)
A very common question is whether it is legitimate to use Likert scale data in parametric statistical procedures that 
require interval data, such as Linear Regression, ANOVA, and Factor Analysis.
A typical Likert scale item has 5 to 11 points that indicate the degree of something. For example, it could measure agreement with a statement, such as 1=Strongly Disagree to 5=Strongly Agree. It can be a 1 to 5 scale, 0 to 10, etc. (more…)
You may have heard that using SPSS syntax is more efficient, gives you more control, and ultimately saves you time and frustration. It’s all true.
….And yet you probably use SPSS because you don’t want to code. You like the menus.
I get it.
I like the menus, too, and I use them all the time.
But I use syntax just as often.
At some point, if you want to do serious data analysis, you have to start using syntax. (more…)