There are two oft-cited assumptions for Analysis of Covariance (ANCOVA), which is used to assess the effect of a categorical independent variable on a numerical dependent variable while controlling for a numerical covariate:
1. The independent variable and the covariate are independent of each other.
2. There is no interaction between independent variable and the covariate.
In a previous post, I showed a detailed example for an observational study where the first assumption is irrelevant, but I have gotten a number of questions about the second.
So what does it mean, and what should you do, if you find an interaction between the categorical IV and the continuous covariate?
Once again, rather than focus on the “rules”, think about what an interaction tells you about the effects of the independent variable, and how you can best communicate the results.
In this (real) example, adult learners were assigned to one of four educational conditions: a control and three experimental conditions. The outcome variable is satisfaction with their training experience and each condition implemented a specific learning strategy. Participants’ age was used as a covariate, as previous research indicated that it is related to satisfaction.
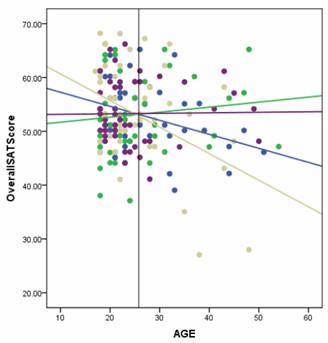Here is a graph of the actual results. The colored lines indicate the association between age and satisfaction within each of the four experimental groups. The purple line is the control group.
As they’re regression lines, the height of each line at a specific age can be interpreted as the mean value of satisfaction at that age for that specific group. So, for example, you can see that the mean satisfaction score is just about equal in all four groups at the point where the four lines cross, around age 25. (Incidentally, the fact that they all cross at the same age is a coincidence—this doesn’t have to happen).
The vertical black line at Age=25.8 represents the mean age of all participants. There were no significant differences in the mean age across groups, indicating that random assignment worked well.
It should be quite clear that the four lines are not parallel. This means that the relationship between age and satisfaction is not the same in every condition.
The p-value for the interaction between age and experimental group was .011. Quite significant.
Clearly, the ANCOVA assumption of parallel lines is not being met.
Okay, what does this mean for the analysis, and more importantly, the conclusions we draw about the data?
What the interaction says about the data
In the control condition and the green condition, age isn’t really related to satisfaction. Whether a participant is 20 or 50, the mean satisfaction is around 55. Yes, it’s slightly higher in the green group at higher ages, but by very little.
But in the blue and tan groups, there is an association between age and satisfaction. As a general pattern, young people tended to like their educational experience. Older people didn’t.
This effect is stronger in the tan group, but it’s there for both. There must have been something in those training programs that appealed more to young people.
This result is very interesting. If I am going to design a new training using one of these four strategies, and I know my audience is generally in their 20s, these results indicate that it really doesn’t matter which strategy I design it around. The mean satisfaction is pretty much equal for young participants.
But if my audience is in their 40s and 50s, the strategy is going to make a difference. If I use that tan strategy, my satisfaction ratings are likely to be pretty low. So I’ll probably get better ratings with the control strategy or the green one.
In other words, the effect of the learning strategy on satisfaction is different for different age participants.
Even if I didn’t hypothesize that, that’s an interesting and useful conclusion.
The parallel lines assumption in ANCOVA
This is the point at which I usually get questions about what to do because a reviewer or committee member insists that ANCOVA can only be used if the lines are parallel.
This is true if the purpose of ANCOVA is to reduce error variation and allow us to report a single, overall effect of the independent variable on the dependent variable, at every value of the covariate.
It’s true that we can’t do that. We have already found that there is not a single effect of learning strategy treatment on satisfaction across all ages. We have to take age into account.
It doesn’t mean that random assignment didn’t work and it doesn’t mean that you should drop the covariate or the interaction term.
All it means is that you cannot:
1) Run the unique model without an interaction that many people mean when they say “ANCOVA.” We know that wouldn’t reflect the data.
2) describe the effect of the IV (training strategy) on the DV without also including some information about age.
Any stat software will allow you to get multiple-testing-adjusted p-values at specific values of a covariate. So it’s very easy to describe, and test, mean differences among the experimental groups at specific ages.
What analysis to do then? Your options:
1. Run just a one-way ANOVA, dropping the covariate.
But do this only if really, truly, the only thing you’re interested in is whether these experimental conditions show differences in satisfaction, regardless of age. The one-way ANOVA will reflect the effects of the treatment groups, regardless of age.
Of course, the main effect for condition in this full model with the interaction will test the same thing, as well as give you additional information at different ages. It is an option, but not necessarily a good one. So your second option is:
2. Run the full model with the interaction, describe the results in detail, and don’t call it ANCOVA to appease reviewers.
I personally tend to advocate this approach, as it really tells the full story of what is going on with your data. But I concede that there are situations where the focus is very narrow and the full story is not of interest.
So whether it is correct to include the covariate and interaction in the model or to drop them both depends on what you really want to know about your data. They are answering different research questions.
But including the interaction term is not wrong because it doesn’t meet an assumption. The assumption is more about defining which models we can call ANCOVA than it is about which models best fit the data.
Hi Karen
Thanks for your article. I really don’t see why the first option “Run just a one-way ANOVA, dropping the covariate” is suggested at all. If there is an interaction between the covariate and the treatment then of course a model including this interaction is the best option. However, if we can only decide between ANOVA and ANCOVA, then I would still go for the ANCOVA as it might at least explain part of the covariate effect where as the ANOVA ignores that completely and therefore is the least accurate model.
Best,
Reto
Hi Karen, very nice article. There are many scenarios. I will give you a tricky one. I have an ANCOVA with one covariate and one categorical variable with 4 levels. One of these levels doesn´t have a significant linear relationship between the IV and the DV. One of the assumptions of ANCOVA is that the covariate and the DV are linearly related. Then, is it ok to drop this level from the analysis and consider only the levels with the significant linear relationship? I will appreciate your advice. Best, GA
You mean for one category, the relationship between Y and the covariate is curved, rather than linear?
In a case like that, I would ignore the “assumptions of ANCOVA” and fit an interaction between the categorical predictor and the covariate squared. It will be a complicated model, but it will fit the data better.
Does this method work with a categorical IV (group) and categorical covariate (gender) with a continuous DV?
Hi Karen,
This was really helpful, thank you. I have a theoretical (and probably very silly) question.
I am looking at whether some cognitive scores (DV) differ across three groups (IV) and I am including age, gender and education as covariates (CVs). I have included the interactions between CV and the IV in the model to check for the homogeneity of regression slopes assumption. I am unsure of how to deal with one specific scenario: the assumption is met (none of the interaction is significant) and, in the same way, the main effect of group is not significant. However, if I re-run the analyses with the same IV, DV and CVs but removing the CVxIV interaction from the model, the effect of the group becomes significant (i.e. there is a significant difference in the cognitive score across groups). I am not sure how to interpret this and which would be the most rigorous way to proceed.
I hope it makes sense and thanks in advance for your kind help.
Kind regards,
Flaminia
Flaminia,
I can’t really give advice without seeing the actual results. There’s too much nuance. But I would suggest really looking at the means and mean differences here, rather than just the p-values. If those interaction terms have effects very close to 0, it’s reasonable to take them out.
Hello
I want to know can I apply the Rank ANCOVA by SPSS if the assumptions of ANCOVA not fulfilled?
Hi Karen,
Great article thank you! I have some data that looks similar to above, however when I run this code:
DATASET ACTIVATE DataSet1.
UNIANOVA Maxinitial BY Pheno WITH AAE
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/EMMEANS=TABLES(Pheno) WITH(AAE=30) COMPARE ADJ(BONFERRONI)
/EMMEANS=TABLES(Pheno) WITH(AAE=MEAN) COMPARE ADJ(BONFERRONI)
/EMMEANS=TABLES(Pheno) WITH(AAE=80) COMPARE ADJ(BONFERRONI)
/PRINT ETASQ DESCRIPTIVE HOMOGENEITY
/CRITERIA=ALPHA(.05)
/DESIGN=AAE Pheno.
I get the same mean differences (and significance) between the groups even though the lines on the scatter plot are clearly far from each other at AAE 30 (age at entry to study) but then converge at AAE=80. Maybe I am misinterpreting what EM means are but I thought they simply reflect the mean value of Y at any value of X based on that groups regression line. Is that correct? If so why do I not see differences between the AAE 30 and 80 when there is a clear difference in the scatter plot?
Many thanks,
Phil
Hi Phil,
It’s because you didn’t include the interaction between Pheno and AAE in the model. By doing that, you’re forcing the model to make the regression lines parallel and the EMMeans reflect that.
Hi Karen,
How silly of me, I did not look carefully enough at your code!
Thank you for your advice, your website really is fantastic!
Phil
Thanks, Phil!
Can you use an ANCOVA to treat one technically “categorical” variable as a continuous variable? This, of course, treats it as a covariate rather than something you control. Is there a more appropriate test for when you have a continuous dependent variable and 1 continuous and 1 categorical independent variable?
Hi Rebecca,
Not really. The problem isn’t about whether it’s a manipulated variable vs. and observed one. It’s about fitting a line when it doesn’t make sense. If you treat a categorical predictor as a numerical one, you’re saying that the difference in its value from 1 to 2 is equal to the difference from 2 to 3, and so on. That’s not true for categorical variables.
But yes, regression and ANCOVA (which are really the same thing) can run a model with one categorical and one continuous predictor. Just search “dummy coding” on this site and you’ll find lots of info. You may also want to check out our free webinar recording on interpreting regression coefficients. There is an example in there like that. https://thecraftofstatisticalanalysis.com/interpreting-linear-regression-coefficients/
Hi, very nice article. I have one theoretical question. Suppose that we do the post hoc test to check differences between slope and it reports that slopes of blue and yellow lines (from the example picture) are not significantly different. Is there any good way to check if their intercepts are different? Run the separate model, with data only from this two groups and do not include interactions in it?
Mikolaj, the coefficients for Condition (there will be 3 for the dummy coded groups) directly test whether the intercepts are different. So as long as the reference category is either the blue or yellow line, you’ll get a direct test of their intercepts.
I would also love to know how you would call the model if you can’t call it ANCOVA. Possibly simply GLM?
Yes, or simply a regression.
Hello, how do I proceed if I want to do a post hoc test to evaluate the difference in the slopes and to check which slopes are significantly different?
I also wanted to ask you how I might reference this page?
Many Thanks,
Charlotte
Hi Karen,
This has been really useful. I’m just wondering what might you call it if not ANCOVA? Additionally, what kind of detail should you report if you go ahead with the analysis and including the interaction?
Thanks,
Charlotte
Thank you for the clarification! Like Susel, this has been driving me crazy. Your posts are really helpful – most of the time they get right to the heart of my questions without me hacking through a jungle of details for one piece of information. I’m so relieved when I google my questions and theanalysisfactor.com pops up in the results 🙂
Hi Karen
Many thanks for this, it is of great help for my doctoral research! I have been going crazy with my analysis not meeting assumptions and the likes. I do have a question. How do you deal with a model where there are 4 covariates and they are highly correlated please? When run the analysis with the predictor (kind of downsizing event) and only one covariate at a time (say perception of senior leaders’ effectiveness or perception of procedural fairness), the effect of the downsizing event on organisational commitment (DV) is significant as is the effect of the covariate and the interaction.
However, when I combine the 4 analyses and use main effects of predictors, the 4 covariates and the interaction between predictor*covariates it all goes pear-share and I don’t know how to interpret the results. In some cases the effect of the predictor becomes non-significant as well as the effect of one or two covariates and certainly most of the interactions become n.sig too.
What would you recommend please? The reason I am throwing everything into the same analysis is because it is a more accurate reflection of what happens in real life (all these things interact)…but it is very complicated! My study is non-experimental. Many thanks!