The linear model normality assumption, along with constant variance assumption, is quite robust to departures. That means that even if the 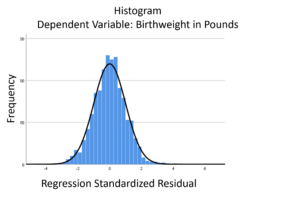 assumptions aren’t met perfectly, the resulting p-values and confidence intervals will still be reasonable estimates.
assumptions aren’t met perfectly, the resulting p-values and confidence intervals will still be reasonable estimates.
This is great because it gives you a bit of leeway to run linear models, which are intuitive and (relatively) straightforward. This is true for both linear regression and ANOVA.
You do need to check the assumptions anyway, though. You can’t just claim robustness and not check. Why? Because some departures are so far off that the p-values and confidence intervals become inaccurate. And in many cases there are remedial measures you can take to turn non-normal residuals into normal ones.
But sometimes you can’t.
Sometimes it’s because the dependent variable just isn’t appropriate for a linear model. The (more…)
 I recently received a great question in a comment about whether the assumptions of normality, constant variance, and independence in linear models are about the errors, εi, or the response variable, Yi.
I recently received a great question in a comment about whether the assumptions of normality, constant variance, and independence in linear models are about the errors, εi, or the response variable, Yi.
The asker had a situation where Y, the response, was not normally distributed, but the residuals were.
Quick Answer: It’s just the errors.
In fact, if you look at any (good) statistics textbook on linear models, you’ll see below the model, stating the assumptions: (more…)
 What are the assumptions of linear models? If you compare two lists of assumptions, most of the time they’re not the same.
What are the assumptions of linear models? If you compare two lists of assumptions, most of the time they’re not the same.
(more…)
Have you ever compared the list of model assumptions for linear regression across two sources? Whether they’re textbooks, lecture  notes, or web pages, chances are the assumptions don’t quite line up.
notes, or web pages, chances are the assumptions don’t quite line up.
Why? Sometimes the authors use different terminology. So it just looks different.
And sometimes they’re including not only model assumptions, but inference assumptions and data issues. All are important, but understanding the role of each can help you understand what applies in your situation.
Model Assumptions
The actual model assumptions are about the specification and performance of the model for estimating the parameters well.
1. The errors are independent of each other
2. The errors are normally distributed
3. The errors have a mean of 0 at all values of X
4. The errors have constant variance
5. All X are fixed and are measured without error
6. The model is linear in the parameters
7. The predictors and response are specified correctly
8. There is a single source of unmeasured random variance
Not all of these are always explicitly stated. And you can’t check them all. How do you know you’ve included all the “correct” predictors?
But don’t skip the step of checking what you can. And for those you can’t, take the time to think about how likely they are in your study. Report that you’re making those assumptions.
Assumptions about Inference
Sometimes the assumption is not really about the model, but about the types of conclusions or interpretations you can make about the results.
These assumptions allow the model to be useful in answering specific research questions based on the research design. They’re not about how well the model estimates parameters.
Is this important? Heck, yes. Studies are designed to answer specific research questions. They can only do that if these inferential assumptions hold.
But if they don’t, it doesn’t mean the model estimates are wrong, biased, or inefficient. It simply means you have to be careful about the conclusions you draw from your results. Sometimes this is a huge problem.
But these assumptions don’t apply if they’re for designs you’re not using or inferences you’re not trying to make. This is a situation when reading a statistics book that is written for a different field of application can really be confusing. They focus on the types of designs and inferences that are common in that field.
It’s hard to list out these assumptions because they depend on the types of designs that are possible given ethics and logistics and the types of research questions. But here are a few examples:
1. ANCOVA assumes the covariate and the IV are uncorrelated and do not interact. (Important only in experiments trying to make causal inferences).
2. The predictors in a regression model are endogenous. (Important for conclusions about the relationship between Xs and Y where Xs are observed variables).
3. The sample is representative of the population of interest. (This one is always important!)
Data Issues that are Often Mistaken for Assumptions
And sometimes the list of assumptions includes data issues. Data issues are a little different.
They’re important. They affect how you interpret the results. And they impact how well the model performs.
But they’re still different. When a model assumption fails, you can sometimes solve it by using a different type of model. Data issues generally stay around.
That’s a big difference in practice.
Here are a few examples of common data issues:
1. Small Samples
2. Outliers
3. Multicollinearity
4. Missing Data
5. Truncation and Censoring
6. Excess Zeros
So check for these data issues, deal with them if the solution doesn’t create more problems than you solved, and be careful with the inferences you draw when you can’t.
Go to the next article or see the full series on Easy-to-Confuse Statistical Concepts
Transformations don’t always help, but when they do, they can improve your linear regression model in several ways simultaneously.
They can help you better meet the linear regression assumptions of normality and homoscedascity (i.e., equal variances). They also can help avoid some of the artifacts caused by boundary limits in your dependent variable — and sometimes even remove a difficult-to-interpret interaction.
(more…)
 There are two oft-cited assumptions for Analysis of Covariance (ANCOVA), which is used to assess the effect of a categorical independent variable on a numerical dependent variable while controlling for a numerical covariate:
There are two oft-cited assumptions for Analysis of Covariance (ANCOVA), which is used to assess the effect of a categorical independent variable on a numerical dependent variable while controlling for a numerical covariate:
1. The independent variable and the covariate are independent of each other.
2. There is no interaction between independent variable and the covariate. (The slopes of the lines between the response and the covariate are parallel).
In a previous post, I showed a detailed example for an observational study where the first assumption is irrelevant, but I have gotten a number of questions about the second.
So what does it mean, and what should you do, if you find an interaction between the categorical IV and the continuous covariate? (more…)
 assumptions aren’t met perfectly, the resulting p-values and confidence intervals will still be reasonable estimates.
assumptions aren’t met perfectly, the resulting p-values and confidence intervals will still be reasonable estimates.

