When we think about model assumptions, we tend to focus on assumptions like independence, normality, and constant variance. The other big assumption, which is harder to see or test, is that there is no specification error. The assumption of linearity is part of this, but it’s actually a bigger assumption.
What is this assumption of no specification error?
The basic idea is that when you choose a final model, you want to choose one that accurately represents the real relationships among variables.
There are a few common ways of specifying a linear model inaccurately.
Specifying a linear relationship between X & Y when the relationship isn’t linear
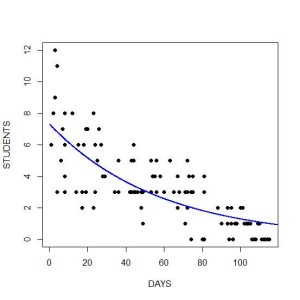It’s often the case that the relationship between a predictor X and Y isn’t a straight line. Let’s use a common one as an example: a curvilinear relationship.
Specifying a line when the relationship is really a curve will result in less-than-optimal model fit, non-independent residuals, and inaccurate predicted values.
One way to check for a curvilinear relationship is with bivariate graphing before you get started modeling. Many times (though not always) the fix is simple: a log transformation of X or an addition of a quadratic (X squared) term.
Other ways to find it include residual graphs and, if they make theoretical sense, adding transformations of X to the model and assessing model fit.
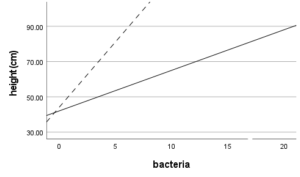Another example is an interaction term.
If the effect of a variable X is moderated by another predictor, it means X doesn’t have a simple linear relationship with Y. X’s relationship with Y depends on the value of a third variable–the moderator.
Including that interaction in the model will accurately represent the real relationship between X and Y. Failing to include it means mis-specification of X’s real effect.
Leaving out important predictors
The basic idea here is that if you’ve left out some important predictor or covariate, your model isn’t an accurate representation.
On the other hand, it’s impossible to realistically include every predictor that predicts or explains the outcome, as much as you may want to.
(And there are certainly models whose job is not to represent all predictors of an outcome. Rather it’s to test the relationship with specific predictors).
So you have to be comfortable with some level of specification error here and focus on minimizing it.
One of the most problematic mistakes here is to leave out an important confounding variable. Of course, you’re limited to the variables in your data set. So this is something to think about long before you’ve collected data.
Including unimportant predictors in the model
Just to make sure this doesn’t get too easy, another cause of model mis-specification is including predictors that are unrelated to the outcome variable.
So we can’t avoid missing an important predictor by throwing every possible predictor we have into the model.
There are many ways to build a model. The goal of all of them is to find the best model. The best model is one that includes all the important predictors in the right form, but not any unimportant ones.
Consequences of specification error
Specification error often, but not always, causes other assumptions to fail.
For example, sometimes you can solve non-normality of the residuals by adding a missed covariate or interaction term.
So the first step in solving problems with other assumptions is usually not to jump to transformations or some other complicated modeling, but to reassess the predictors you’ve put into the model.
Leave a Reply