When you’re model building, a key decision is which interaction terms to include. And which interactions to remove.
As a general rule, the default in regression is to leave them out. Add interactions only with a solid reason. It would seem like data fishing to simply add in all possible interactions.
And yet, that’s a common practice in most ANOVA models: put in all possible interactions and only take them out if there’s a solid reason. Even many software procedures default to creating interactions among categorical predictors.
Rather than ponder why we approach these differently or which is right, in this article I want to explain what it really means when an interaction is or is not in a model. It can be a bit counter-intuitive.
An Example
Let’s use this (made up) example from one of my website articles:
A model of the height of a shrub (Height) based on the amount of bacteria in the soil (Bacteria) and whether the shrub is located in partial or full sun (Sun).
Height is measured in cm; Bacteria is measured in thousand per ml of soil; and Sun = 0 if the plant is in partial sun, and Sun = 1 if the plant is in full sun.
Here’s the model without an interaction term: Height = 42 + 2.3*Bacteria + 11*Sun
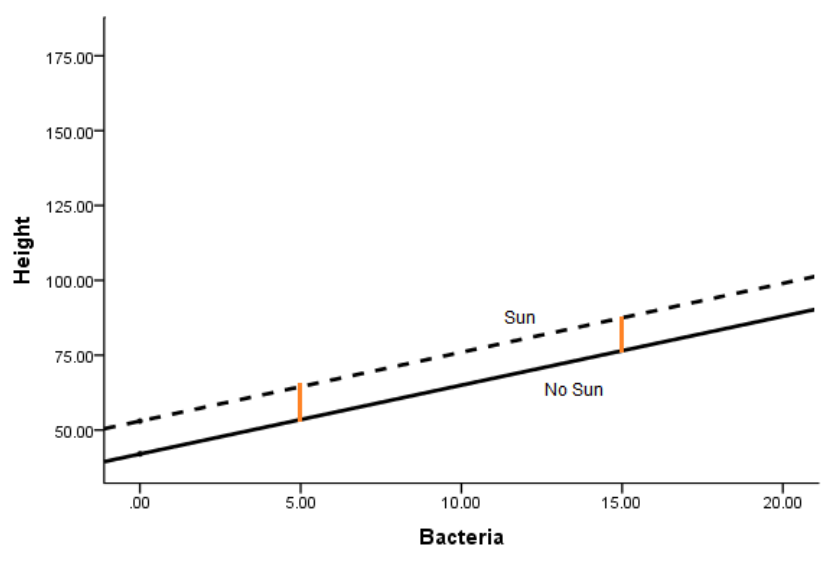
And here is the model with one: Height = 35 + 1.2*Bacteria + 9*Sun + 3.2*Bacteria*Sun
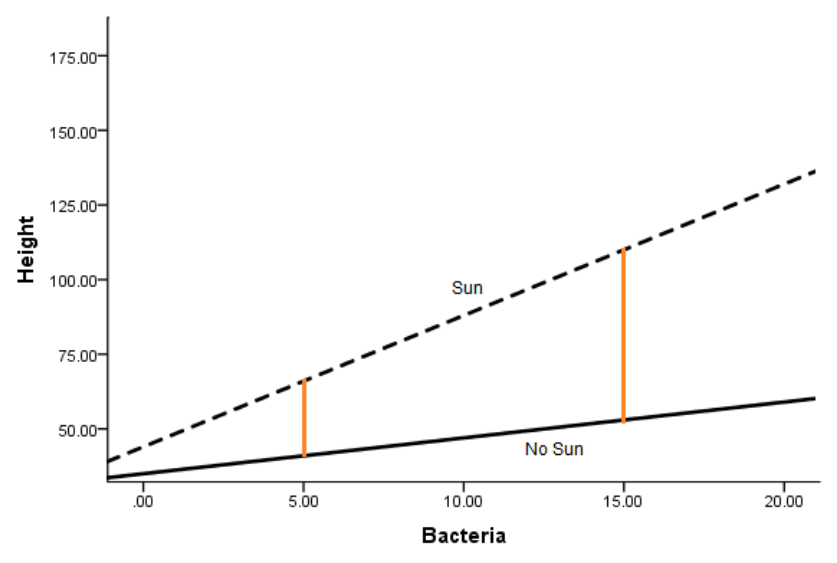
There are a few things you can see here:
1. Adding the interaction allows the effect (slope) of Bacteria to differ in the two Sun conditions
2. It also allows the effect (mean difference) in the Sun condition (the height of the orange lines) to differ at different values of Bacteria.
3. The interaction coefficient itself (3.2) estimates this difference in effect for one predictor, depending on the value of the other.
If it turns out that the best estimate of the interaction coefficient was zero, not 3.2, then the bottom graph would have looked like the top one.
What happens when you remove an interaction from a model
And here’s the counter-intuitive part:
When you include an interaction in a model, you’re estimating that coefficient from the data. Sometimes the estimate will be zero, or very close to zero, and sometimes not.
When you don’t specify an interaction term, the difference in effects doesn’t just go away. That difference always exists. By not specifying that you want the software to estimate the difference in those effects, you are setting it to zero.
Counter-intuitive, right? By not specifying it, you’re actually taking a more active stance: setting it to zero.
This is, incidentally, the same issue with removing an intercept from a model, when it theoretically should be zero or is not statistically different from zero.
In the case of the intercept, the general consensus is removing it will lead to unacceptable bias and poor fit. It’s a rare situation where removal is worthwhile.
Technically, the same is true for interactions, but they are generally held to a different standard. Why? First, interactions are often a little more exploratory in their nature. Second, they add more complexity to a model.
As with all issues of model complexity, sometimes the better coefficient estimates and model fit are worth it and sometimes they aren’t. Whether the complexity is worth it depend on the hypotheses, the sample size, and the purpose of the model.
So should you always include interactions to a model? No, but it’s always a good practice to stop and think about what it means to leave them out and whether that’s really what you want to test.


I was thinking about this issue a few months ago while reviewing articles on so-called “questionable research practices” (QRPs; e.g., HARKing, fishing expeditions, data-driven decision making, etc.). Those articles typically discuss QRPs in the context of regression models, but it seemed to me that ANOVA is not immune to the same problems. It then occurred to me that one could use a hierarchical approach to ANOVA as follows:
Block 1: Include only those terms needed to address a priori hypotheses.
Block 2: Full factorial model.
Only Block 1 results should be treated as confirmatory (or as close to it as one can get); Block 2 results should be treated as exploratory.
I don’t know if this approach has been proposed in any books or articles, but I’ve not come across it so far.
In my class dealing with designed experiment I use the motto ‘Analyze them as you randomized them’, making clear that the analysis should follow the design. People who teach otherwise are unclear why we design experiments. Designed experiments have too many advantages to count, chief among them is that we don’t have to hunt for confounding sources of variation. As far a regression in multi-factor experiments Piepho and Edmondsons (2018) published ‘A tutorial on the statistical analysis of factorial experiments with qualitative and quantitative treatment factor levels’ in J. of Agronomy and Crop Science, which is a nice teaching tool. As far as dropping effects from the model is concerned, that variation has to go somewhere. Caveat emptor is the motto here.
I think the difference in typical specifications between anova and regression is often due to anova models tending to have a small number of variables and regressions tending to have many many, so the full factorial model is more tractable in the anova case.
You might be interested in an article I published some time ago,
Turner, David L. (1990) ‘An easy way to tell what you are esting
in analysis of variance’, Communications in Statistics – Theory and Methods, 19:12,
4807 – 4832
The results apply to generalized models as well.
Reader’s Digest version: Leaving terms out of linear type models adjusts least squares means to NOT have those effects. Then tests are done on the ADJUSTED means.
I was always taught that when interpreting the results of an ANOVA with interactions one should interpret the interactions first before considering the results of the main effects. When doing so, one should also look at the most complex interaction first before moving to the less complex ones and finally looking at the main effects.
As you indicated the critical step with this whole issue is teaching how to interpret the results of the analysis and not just to focus on the selection and procedure of conducting a statistical procedure.