Predictor variables in statistical models can be treated as either continuous or categorical.
Usually, this is a very straightforward decision.
Categorical predictors, like treatment group, marital status, or highest educational degree should be specified as categorical.
Likewise, continuous predictors, like age, systolic blood pressure, or percentage of ground cover should be specified as continuous.
But there are numerical predictors that aren’t continuous. And these can sometimes make sense to treat as continuous and sometimes make sense as categorical.
Let’s look at a few examples.
Discrete Predictor Variables
Count predictor variables, like number of therapy sessions or number of symptoms, are numerical but not continuous. They can have whole, positive values, but not decimals.
Another type of discrete variable is when truly continuous variables are only measured at discrete intervals. For example, in longitudinal studies, time is often measured at discrete points: 1 week, 2 weeks, 4 weeks, 8 weeks, 16 weeks post treatment. Time could have been continuous had it been measured in days, hours, or minutes, but here it wasn’t.
This also happens in data sets where a potentially continuous variable has few values in the data set, intentionally or not. For example, when every single individual in the data set has one of three possible ages: 6, 8, and 10.
A clarification: I am not talking about grouping numerical values into categories, like all ages above 8 = old and all ages below 8 = young. I’m talking about making each value of age its own category.
If you specify a predictor as continuous, the software will fit a best-fitting regression line between that predictor and Y, the response variable, after accounting for other variables in the model. The coefficient of that predictor is a slope of the regression line (shown in red).
Because a discrete predictor is numerical, fitting a line to it can be reasonable. Its values are true numbers with meaningful intervals between them.
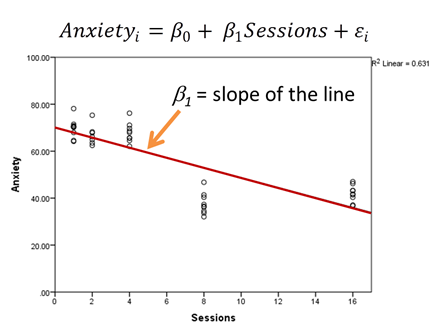
If you specify a predictor as categorical, the software will estimate a mean of Y for each category of the predictor (shown below in red). There will be a set of coefficients for that predictor. Each one measures the difference in the means of Y between one category of X and the reference category.
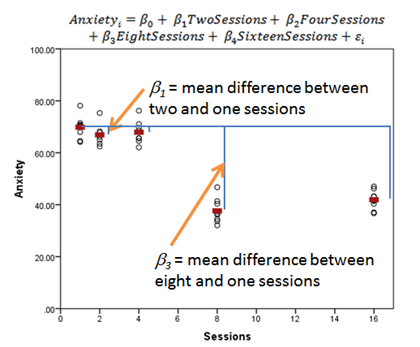
Considerations
So which do you use?
As always, it depends.
A few things to keep in mind as you decide:
-
Is your research question about a constant change over X or is it specifically about mean differences at specific values of X?
If it’s the former, fitting a line makes more sense. If it’s the latter, fitting a set of mean differences makes more sense. The whole point of your analysis is to answer a research question.
-
How many discrete values of X are there?
You need a minimum of 3 values of X to fit a line, but with only 3, it can be hard to tell if there really is a linear trend. The more values of X, the more cumbersome it is to have a set of mean differences and the more clearly you can fit a line (or a curve).
-
Is the actual relationship linear?
In our example, it isn’t so linear. Instead it looks like there is a jump downward somewhere between 4 and 8 weeks. It may not be realistic to fill in the times between our 5 measured times with a constant slope.
A set of 5 means may better tell the story in the data. A follow-up study with more time points may tell us a more complete story about whether there is a jump downward somewhere between 4 and 8 sessions or if there is a curve or straight line downward between 4 and 8.


Leave a Reply