Non-parametric ANOVA in SPSS

I sometimes get asked questions that many people need the answer to.  Here’s one about non-parametric ANOVA in SPSS.

Question:

Is there a non-parametric 3 way ANOVA out there and does SPSS have a way of doing a non-parametric anova sort of thing with one main independent variable and 2 highly influential cofactors?

Quick Answer:

No.

Detailed Answer:

There is a non-parametric one-way ANOVA: Kruskal-Wallis, and it’s available in SPSS under non-parametric tests.  There is even a non-paramteric two-way ANOVA, but it doesn’t include interactions (and for the life of me, I can’t remember its name, but I remember learning it in grad school).

But there is no non-parametric factorial ANOVA, and it’s because of the nature of interactions and most non-parametrics.

What it basically comes down to is that most non-parametric tests are rank-based. In other words, instead of using the actual Y values, the test is based on ordering, ranking, and comparing the group’s ranks of all those Y values.

This works very well in any one-way comparison. You can compare the relative rankings of two or more 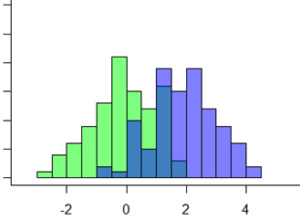groups. This shows if one group’s distribution is generally shifted left or right, in comparison to the others.

But it doesn’t tell you how much the distribution is shifted.  Just that its values are generally higher or lower.  In order to distinctly measure how much shift we had, we’d need to measure the shift in one distribution parameter.

In ANOVA, we use the means as that parameter, but the whole point in a non-parametric test is to not use a parameter.

So in ANOVA, we directly measure how different two or more means are.

Being able to measure the size of this difference is especially important for interactions, because an interaction is asking if the mean difference for one factor is the same for all values of the other factor.  If we can’t quantify the size of the difference, we can’t test the interaction.

So as long as you’re not trying to include interactions, a rank-based non-parametric test will work just fine.  If you are, then it’s just not going to work.

Getting Started with SPSS

Karen will introduce you to how SPSS is set up, some hidden features to make it easier to use, and some practical tips.

Take Me to The Video!