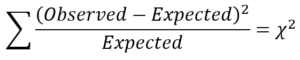independence

The Difference between Chi Square Tests of Independence and Homogeneity

A chi square test is often applied to two-way tables, like the one below.

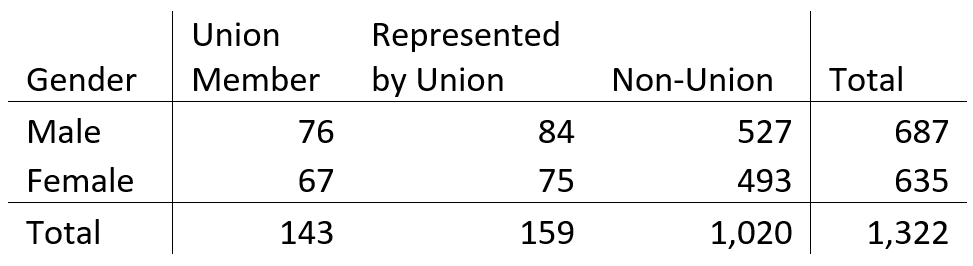
A table of Union Status by Gender for Employed Individuals in 2020 (adapted from Current Population Survey, Bureau of Labor Statistics)

This table represents a sample of 1,322 individuals. Of these individuals, 687 are male, and 635 are female. Also 143 are union members, 159 are represented by unions, and 1,020 are not affiliated with a union.

You might use a chi-square test if you want to learn something about the relationship of gender and union status. The question then might come up: should you use a test of independence, or a test of homogeneity?

Does it matter? Software doesn’t generally differentiate between the two, which leads to a final question: are they even different?

Well, yes and no. Read on!

Different: Independence versus Homogeneity

Independence and homogeneity do refer to different ideas. If union status and gender are independent, that means that union status and gender are unrelated. In other words, if you know someone’s union status, you won’t be able to make a better guess as to their gender.

If you know someone’s gender, you won’t be able to make a better guess as to their union status.

Homogeneity is different and refers to the concept of similarity. If you are familiar with linear regression, you might associate this with residuals. Residuals should be homogeneous, meaning they all come from the same distribution.

That idea applies to this two-way table as well. We may want to know if the distribution of union status is the same for men and women. In other words, does union status come from the same distribution for both men and women?

To test independence, we would not approach the question from the standpoint of gender or union status. We would take a sample of all employed individuals, and then break them down into the categories in the table.

To test homogeneity, we would approach it from the standpoint of gender. We would randomly sample individuals from within each gender, and then measure their union status.

Either approach would result in the table above.

Same: Chi-Square Statistics

Chi-square statistics for categorical data generally follow this formula:

For each of the six cells representing a combination of gender and union status, the number in the cell is the count we observe. “Expected” refers to what we would see in each cell under the null hypothesis. That means if gender and union status are independent (or if union status is homogeneous across the genders).

We calculate the difference, square it, and divide by the expected count for each cell. We then add these all together, and that is the chi-square test statistic.

Where do we get the expected counts for each cell?

Let’s examine the combination of male and union member under independence. If gender and union membership are independent, then how many male union members do we expect? Well,
– 10.81% of the sample are union members
– 51.96% are male

So, if they are independent, 10.81% x 51.96% is 5.62%, and 5.62% of 1,322 is 74.3. This is how many individuals we would expect to be male union members.

Now let’s consider male union members under homogeneity. Overall, 10.81% of the sample are union members. If this is the same for both males and females, then of the 687 males, we expect 74.3 to be union members.

Independence and homogeneity result in the same expected number of union members! It turns out this calculation is the same for every cell in the table. It follows that the chi-square statistic is also the same.

Does It Matter?

As it turns out, independence and homogeneity are two sides of the same coin. If gender and union status are independent, then union status is distributed the same way for males and females.

So which test should you say you are using, if they turn out the same?

Again, that comes back to how you have phrased your research question. Are you determining whether gender and union status are related. That is a test of independence. Are you looking for differences between males and females? That is a test of homogeneity.

What is a Chi-Square Test?

by Karen Grace-Martin Leave a Comment

Just about everyone who does any data analysis has used a chi-square test. Probably because there are quite a few of them, and they’re all useful.

But it gets confusing because very often you’ll just hear them called “Chi-Square test” without their full, formal name. And without that context, it’s hard to tell exactly what hypothesis that test is testing. [Read more…] about What is a Chi-Square Test?

Member Training: Seven Fundamental Tests for Categorical Data

by TAF Support

In the world of statistical analyses, there are many tests and methods that for categorical data. Many become extremely complex, especially as the number of variables increases. But sometimes we need an analysis for only one or two categorical variables at a time. When that is the case, one of these seven fundamental tests may come in handy.

These tests apply to nominal data (categories with no order to them) and a few can apply to other types of data as well. They allow us to test for goodness of fit, independence, or homogeneity—and yes, we will discuss the difference! Whether these tests are new to you, or you need a good refresher, this training will help you understand how they work and when each is appropriate to use.

The Proportional Hazard Assumption in Cox Regression

by guest contributer 2 Comments

by Steve Simon, PhD

The Cox regression model has a fairly minimal set of assumptions, but how do you check those assumptions and what happens if those assumptions are not satisfied?

Non-proportional hazards

The proportional hazards assumption is so important to Cox regression that we often include it in the name (the Cox proportional hazards model). What it essentially means is that the ratio of the hazards for any two individuals is constant over time. They’re proportional. It involves logarithms and it’s a strange concept, so in this article, we’re going to show you how to tell if you don’t have it.

There are several graphical methods for spotting this violation, but the simplest is an examination of the Kaplan-Meier curves.

If the curves cross, as shown below, then you have a problem.

Likewise, if one curve levels off while the other drops to zero, you have a problem.

Figure 2. Kaplan-Meier curve with only one curve leveling off

You can think of non-proportional hazards as an interaction of your independent variable with time. It means that you have to do more work in interpreting your model. If you ignore this problem, you may also experience a serious loss in power.

If you have evidence of non-proportional hazards, don’t despair. There are several fairly simple modifications to the Cox regression model that will work for you.

Nonlinear covariate relationships

The Cox model assumes that each variable makes a linear contribution to the model, but sometimes the relationship may be more complex.

You can diagnose this problem graphically using residual plots. The residual in a Cox regression model is not as simple to compute as the residual in linear regression, but you look for the same sort of pattern as in linear regression.

If you have a nonlinear relationship, you have several options that parallel your choices in a linear regression model.

Lack of independence

Lack of independence is not something that you have to wait to diagnose until your data is collected. Often it is something you are aware from the start because certain features of the design, such as centers in a multi-center study, are likely to produce correlated outcomes. These are the same issues that hound you with a linear regression model in a multi-center study.

There are several ways to account for lack of independence, but this is one problem you don’t want to ignore. An invalid model will ruin all your confidence intervals and p-values.