linear regression

If you’ve used much analysis of variance (ANOVA), you’ve probably heard that ANOVA is a special case of linear regression. Unless you’ve seen why, though, that may not make a lot of sense. After all, ANOVA compares means between categories, while regression predicts outcomes with numeric variables.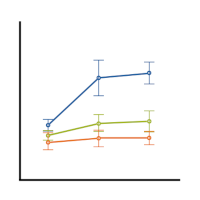 (more…)

No comments yet

A very common question is whether it is legitimate to use Likert scale data in parametric statistical procedures that require interval data, such as Linear Regression, ANOVA, and Factor Analysis.

A typical Likert scale item has 5 to 11 points that indicate the degree of something. For example, it could measure agreement with a statement, such as 1=Strongly Disagree to 5=Strongly Agree. It can be a 1 to 5 scale, 0 to 10, etc. (more…)

52 comments

Centering variables is common practice in some areas, and rarely seen in others. That being the case, it isn’t always clear what are the reasons for centering variables. 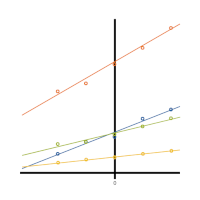Is it only a matter of preference, or does centering variables help with analysis and interpretation? (more…)

No comments yet

When is it important to use adjusted R-squared instead of R-squared?

R², the the Coefficient of Determination, is one of the most useful and intuitive statistics we have in linear regression.

It tells you how well the model predicts the outcome and has some nice properties. But it also has one big drawback.

(more…)

4 comments

Updated 12/20/2021

Despite its popularity, interpreting regression coefficients of any but the simplest models is sometimes, well….difficult.

So let’s interpret the coefficients in a model with two predictors: a continuous and a categorical variable.  The example here is a linear regression model. But this works the same way for interpreting coefficients from any regression model without interactions.

A linear regression model with two predictor variables results in the following equation:

Y_i = B₀ + B₁*X_1i + B₂*X_2i + e_i.

The variables in the model are:

• Y, the response variable;
• X₁, the first predictor variable;
• X₂, the second predictor variable; and
• e, the residual error, which is an unmeasured variable.

The parameters in the model are:

• B₀, the Y-intercept;
• B₁, the first regression coefficient; and
• B₂, the second regression coefficient.

One example would be a model of the height of a shrub (Y) based on the amount of bacteria in the soil (X₁) and whether the plant is located in partial or full sun (X₂).

Height is measured in cm. Bacteria is measured in thousand per ml of soil.  And type of sun = 0 if the plant is in partial sun and type of sun = 1 if the plant is in full sun.

Let’s say it turned out that the regression equation was estimated as follows:

Y = 42 + 2.3*X₁ + 11*X₂

Interpreting the Intercept

B₀, the Y-intercept, can be interpreted as the value you would predict for Y if both X₁ = 0 and X₂ = 0.

We would expect an average height of 42 cm for shrubs in partial sun with no bacteria in the soil. However, this is only a meaningful interpretation if it is reasonable that both X₁ and X₂ can be 0, and if the data set actually included values for X₁ and X₂ that were near 0.

If neither of these conditions are true, then B0 really has no meaningful interpretation. It just anchors the regression line in the right place. In our case, it is easy to see that X₂ sometimes is 0, but if X₁, our bacteria level, never comes close to 0, then our intercept has no real interpretation.

Interpreting Coefficients of Continuous Predictor Variables

Since X₁ is a continuous variable, B₁ represents the difference in the predicted value of Y for each one-unit difference in X₁, if X₂ remains constant.

This means that if X₁ differed by one unit (and X₂ did not differ) Y will differ by B₁ units, on average.

In our example, shrubs with a 5000/ml bacteria count would, on average, be 2.3 cm taller than those with a 4000/ml bacteria count. They likewise would be about 2.3 cm taller than those with 3000/ml bacteria, as long as they were in the same type of sun.

(Don’t forget that since the measurement unit for bacteria count is 1000 per ml of soil, 1000 bacteria represent one unit of X₁).

Interpreting Coefficients of Categorical Predictor Variables

Similarly, B₂ is interpreted as the difference in the predicted value in Y for each one-unit difference in X₂ if X₁ remains constant. However, since X₂ is a categorical variable coded as 0 or 1, a one unit difference represents switching from one category to the other.

B₂ is then the average difference in Y between the category for which X₂ = 0 (the reference group) and the category for which X₂ = 1 (the comparison group).

So compared to shrubs that were in partial sun, we would expect shrubs in full sun to be 11 cm taller, on average, at the same level of soil bacteria.

Interpreting Coefficients when Predictor Variables are Correlated

Don’t forget that each coefficient is influenced by the other variables in a regression model. Because predictor variables are nearly always associated, two or more variables may explain some of the same variation in Y.

Therefore, each coefficient does not measure the total effect on Y of its corresponding variable. It would if it were the only predictor variable in the model. Or if the predictors were independent of each other.

Rather, each coefficient represents the additional effect of adding that variable to the model, if the effects of all other variables in the model are already accounted for.

This means that adding or removing variables from the model will change the coefficients. This is not a problem, as long as you understand why and interpret accordingly.

Interpreting Other Specific Coefficients

I’ve given you the basics here. But interpretation gets a bit trickier for more complicated models, for example, when the model contains quadratic or interaction terms. There are also ways to rescale predictor variables to make interpretation easier.

So here is some more reading about interpreting specific types of coefficients for different types of models:

• Interpreting the Intercept
• Removing the Intercept when X is Continuous or Categorical
• Interpreting Interactions in Regression
• How Changing the Scale of X affects Interpreting its Regression Coefficient
  
• Interpreting Coefficients with a Centered Predictor

31 comments

The practice of choosing predictors for a regression model, called model building, is an area of real craft.

There are many possible strategies and approaches and they all work well in some situations. Every one of them requires making a lot of decisions along the way. As you make decisions, one danger to look out for is overfitting—creating a model that is too complex for the the data. (more…)

1 comment