Have you ever wondered whether you should report separate means for different groups or a pooled mean from the entire sample? This is a common scenario that comes up, for instance in deciding whether to separate by sex, region, observed treatment, et cetera.
OptinMon 10 - 14 Steps
When to Report Separate Group or a Pooled Mean
November 12th, 2024 by guest contributer
The Steps for Running any Statistical Model
September 10th, 2024 by Karen Grace-Martin
No matter what statistical model you’re running, you need to go through the same steps. The order and the specifics of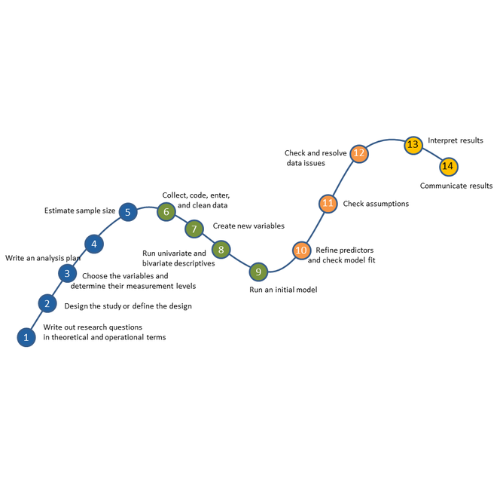 
how you do each step will differ depending on the data and the type of model you use.
These steps are in 4 phases. Most people think of only the third as modeling. But the phases before this one are fundamental to making the modeling go well. It will be much, much easier, more accurate, and more efficient if you don’t skip them.
And there is no point in running the model if you skip phase 4.
If you think of them all as part of the analysis, the modeling process will be faster, easier, and make more sense.
Phase 1: Define and Design
In the first 5 steps of running the model, the object is clarity. You want to make everything as clear as possible to yourself. The more clear things are at this point, the smoother everything will be. (more…)
Seven Steps for Data Cleaning
June 20th, 2024 by Kat Caldwell
Ever consider skipping the important step of cleaning your data? It’s tempting but not a good idea. Why? It’s a bit like baking.
I like to bake. There’s nothing nicer than a rainy Sunday with no plans, and a pantry full of supplies. I have done my shopping, and now it’s time to make the cake. Ah, but the kitchen is a mess. I don’t have things in order. This is no way to start.
First, I need to clear the counter, wash the breakfast dishes, and set out my tools. I need to take stock, read the recipe, and measure out my ingredients. Then it’s time for the fun part. I’ll admit, in my rush to get started I have at times skipped this step.
Too Many Colors Spoil the Graph
March 26th, 2024 by guest contributer
When you draw a graph- either a bar chart, a scatter plot, or even a pie chart, you have the choice of a broad range of colors that you can use. R, for example, has 657 different colors from aliceblue to yellowgreen. SAS has 13 shades of orange, 33 shades of blue, and 47 shades of green. They even have different shades of black.
You have a wealth of colors, but you can’t use all of them in the same graph. The ideal number of colors is 2.
What is Family-wise Error Rate?
December 8th, 2023 by Kat Caldwell
In statistical practice, there are many situations where best practices are clear. There are many, though, where they aren’t. The granddaddy of these practices is adjusting p-values when you make multiple comparisons. There are good reasons to do it and good reasons not to. It depends on the situation.
At the heart of the issue is a concept called Family-wise Error Rate (FWER). FWER is the probability that
The Difference between Standard Deviation and Standard Error
November 10th, 2023 by Karen Grace-Martin
Standard deviation and standard error are statistical concepts you probably learned well enough in Intro Stats to pass the test. Conceptually, you understand them, yet the difference doesn’t make a whole lot of intuitive sense.
So in this article, let’s explore the difference between the two. We will look at an example, in the hopes of making these concepts more intuitive. You’ll also see why sample size has a big effect on standard error. (more…)