Generalized Linear Models in R, Part 5: Graphs for Logistic Regression

by David Lillis, Ph.D.

In my last post I used the glm() command in R to fit a logistic model with binomial errors to investigate the relationships between the numeracy and anxiety scores and their eventual success.

Now we will create a plot for each predictor. This can be very helpful for helping us understand the effect of each predictor on the probability of a 1 response on our dependent variable.

We wish to plot each predictor separately, so first we fit a separate model for each predictor. This isn’t the only way to do it, but one that I find especially helpful for deciding which variables should be entered as predictors.

model_numeracy <- glm(success ~ numeracy, binomial)
 summary(model_numeracy)
Call:
glm(formula = success ~ numeracy, family = binomial)

Deviance Residuals: 
   Min       1Q   Median       3Q     Max 
-1.5814 -0.9060   0.3207   0.6652   1.8266 

Coefficients:
           Estimate Std. Error z value Pr(>|z|)   
(Intercept) -6.1414     1.8873 -3.254 0.001138 ** 
numeracy     0.6243     0.1855   3.366 0.000763 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

   Null deviance: 68.029 on 49 degrees of freedom
Residual deviance: 50.291 on 48 degrees of freedom
AIC: 54.291

Number of Fisher Scoring iterations: 5

We do the same for anxiety.

model_anxiety <- glm(success ~ anxiety, binomial)

summary(model_anxiety)
Call:
glm(formula = success ~ anxiety, family = binomial)

Deviance Residuals: 
   Min       1Q   Median       3Q     Max 
-1.8680 -0.3582   0.1159   0.6309   1.5698 

Coefficients:
           Estimate Std. Error z value Pr(>|z|)   
(Intercept) 19.5819     5.6754   3.450 0.000560 ***
anxiety     -1.3556    0.3973 -3.412 0.000646 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

   Null deviance: 68.029 on 49 degrees of freedom
Residual deviance: 36.374 on 48 degrees of freedom
AIC: 40.374

Number of Fisher Scoring iterations: 6

Now we create our plots. First we set up a sequence of length values which we will use to plot the fitted model. Let’s find the range of each variable.

range(numeracy)
 [1] 6.6 15.7

range(anxiety)
 [1] 10.1 17.7

Given the range of both numeracy and anxiety. A sequence from 0 to 15 is about right for plotting numeracy, while a range from 10 to 20 is good for plotting anxiety.

xnumeracy <-seq (0, 15, 0.01)

ynumeracy <- predict(model_numeracy, list(numeracy=xnumeracy),type="response")

Now we use the predict() function to set up the fitted values. The syntax type = “response” back-transforms from a linear logit model to the original scale of the observed data (i.e. binary).

plot(numeracy, success, pch = 16, xlab = "NUMERACY SCORE", ylab = "ADMISSION")

lines(xnumeracy, ynumeracy, col = "red", lwd = 2)

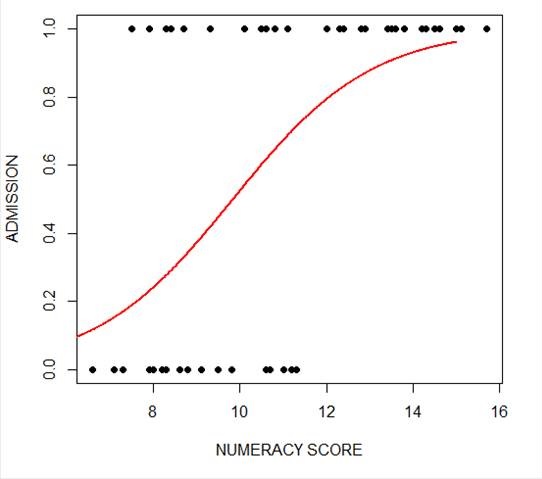The model has produced a curve that indicates the probability that success = 1 to the numeracy score.  Clearly, the higher the score, the more likely it is that the student will be accepted.

Now we plot for anxiety.

xanxiety <- seq(10, 20, 0.1)

yanxiety <- predict(model_anxiety, list(anxiety=xanxiety),type="response")

plot(anxiety, success, pch = 16, xlab = "ANXIETY SCORE", ylab = "SUCCESS")

lines(xanxiety, yanxiety, col= "blue", lwd = 2)

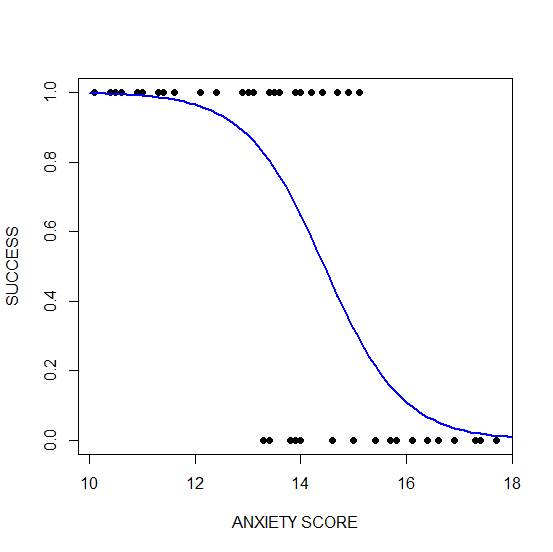Clearly, those who score high on anxiety are unlikely to be admitted, possibly because their admissions test results are affected by their high level of anxiety.

****

See our full R Tutorial Series and other blog posts regarding R programming.

About the Author: David Lillis has taught R to many researchers and statisticians. His company, Sigma Statistics and Research Limited, provides both on-line instruction and face-to-face workshops on R, and coding services in R. David holds a doctorate in applied statistics.

Tagged as: generalized linear models, GLM, Logistic Regression, Predicted probabilitites, R