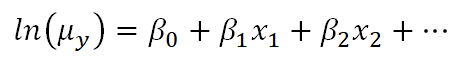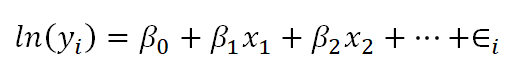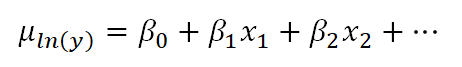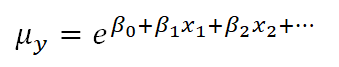Even if you’ve never heard the term Generalized Linear Model, you may have run one. It’s a term for a family of models that includes logistic and Poisson regression, among others.
It’s a small leap to generalized linear models, if you already understand linear models. Many, many concepts are the same in both types of models.
But one thing that’s perplexing to many is why generalized linear models have no error term, like linear models do. (more…)
When we run a statistical model, we are in a sense creating a mathematical equation. The simplest regression model looks like this:
Yi = β0 + β1X+ εi
The left side of the equation is the sum of two parts on the right: the fixed component, β0 + β1X, and the random component, εi.
You’ll also sometimes see the equation written (more…)
Learning statistics is difficult enough; throw in some especially confusing terminology and it can feel impossible! There are many ways that statistical language can be confusing.
Some terms mean one thing in the English language, but have another (usually more specific) meaning in statistics. (more…)
Generalized linear models—and generalized linear mixed models—are called generalized linear because they connect a model’s outcome to its predictors in a linear way. The function used to make this connection is called a link function. Link functions sounds like an exotic term, but they’re actually much simpler than they sound.
For example, Poisson regression (commonly used for outcomes that are counts) makes use of a natural log link function as follows:
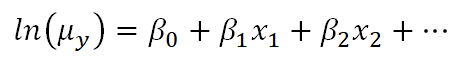
Clearly, there is not a direct linear relationship of the x variables to the average count, but there is a “sort of linear” relationship happening: a function of the mean of y is related to a linear combination of x variables. In other words, the linear model has now been generalized to a bigger type of situation.
This can lead to confusion, though, because on the surface it looks very similar to what happens when we transform the dependent variable in a linear model, like a linear regression.
The key thing to understand is that the natural log link function is a function of the mean of y, not the y values themselves.
Below is a linear model equation where the original dependent variable, y, has been natural log transformed. That is, the natural log has been taken of each individual value of y, and that is being used as the dependent variable.
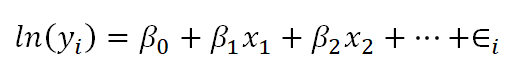
The linear model with the log transformation is providing an equation for an individual value of ln(y). We could also write it as follows, where we are modeling the mean of ln(y) (note the error term is no longer present):
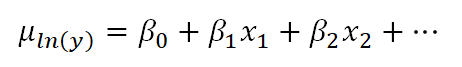
This makes the difference a bit clearer. When we transform the data in a linear model, we are no longer claiming that y is normally distributed around a mean, given the x values — we are claiming that our new outcome variable, ln(yi), is normally distributed.
In fact, we often make this transformation specifically because the values of y do not appear to be normally distributed around their average.
In the case of the Poisson model, however, the link function does not change the distribution of the actual observations in some way to make them something other than Poisson distributed. Instead, the link function defines the relationship of the x variables directly to the mean of the Poisson distributed y. The individual observations then vary around this expected value accordingly.
As you may know, if you have used this kind of data transformation in a linear model before, you cannot simply take the exponent of the mean of ln(y) to get the mean of y.
You might be surprised to know, though, that you can do this with a link function. If you have specific values of your x variables, you can calculate the predicted average count, μy based on those x values by inversing the natural log:
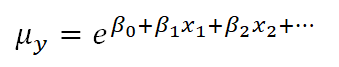
This ability to back-transform means (and regression coefficients) to a more intuitive scale is part of what makes generalized linear models so useful.
Most analysts’ primary focus is to check the distributional assumptions with regards to residuals. They must be independent and identically distributed (i.i.d.) with a mean of zero and constant variance.
Residuals can also give us insight into the quality of our models.
In this webinar, we’ll review and compare what residuals are in linear regression, ANOVA, and generalized linear models. Jeff will cover:
Knowing how to piece this information together will improve your statistical modeling skills.
Note: This training is an exclusive benefit to members of the Statistically Speaking Membership Program and part of the Stat’s Amore Trainings Series. Each Stat’s Amore Training is approximately 90 minutes long.