Even if you’ve never heard the term Generalized Linear Model, you may have run one. It’s a term for a family of models that includes logistic and Poisson regression, among others.
It’s a small leap to generalized linear models, if you already understand linear models. Many, many concepts are the same in both types of models.
But one thing that’s perplexing to many is why generalized linear models have no error term, like linear models do.
Before we explore that, we need to see exactly what that error term is doing in a linear model.
The Error Term in a Linear Model
You’ll often see linear models written two different ways:
They’re not interchangeable, exactly, but they are both accurate. The former models the individual values of the outcome variable, Yi, as the sum of two parts. The first part is the fixed part of the model. It contains all the betas and Xs: β0+β1X1i. The second is the error term, εi.
The fixed part of the model adds up to a mean of Y, conditional on a value of X. The error term measures how far off that data point is from the conditional mean.
So another way of writing the model is to focus on only that fixed part of the model, and write it with the conditional mean only. This is what we see in the second equation. The concept of a conditional mean can seem strange, but it’s simply the mean of Y at each value of X.
The Generalized Linear Model
In a generalized linear model, both forms don’t work. We can’t model the values of Y directly in a linear form. In fact, the closest we can get is to model a function of the conditional mean:
This function is called the link function.
Every generalized linear model has a link function. Which function you use depends on the conditional distribution of Y. For example, a binomial-distributed Y uses a logistic link function and a Poisson-distributed Y uses a natural log.
As you see, neither model has an error term. It’s simply because we’re modeling the mean, not the individual Y values.

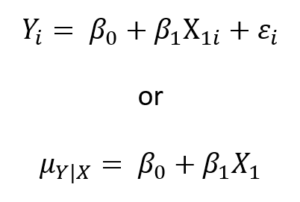
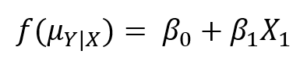
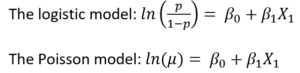

It’s clearly explained.