An incredibly useful tool in evaluating and comparing predictive models is the ROC curve.
Its name is indeed strange. ROC stands for Receiver Operating Characteristic. Its origin is from sonar back in the 1940s. ROCs were used to measure how well a sonar signal (e.g., from an enemy submarine) could be detected from noise (a school of fish).
ROC curves are a nice way to see how any predictive model can distinguish between the true positives and negatives. (more…)
In my last post I used the glm() command in R to fit a logistic model with binomial errors to investigate the relationships between the numeracy and anxiety scores and their eventual success.
Now we will create a plot for each predictor. This can be very helpful for helping us understand the effect of each predictor on the probability of a 1 response on our dependent variable.
We wish to plot each predictor separately, so first we fit a separate model for each predictor. This isn’t the only way to do it, but one that I find especially helpful for deciding which variables should be entered as predictors.
model_numeracy <- glm(success ~ numeracy, binomial)
summary(model_numeracy)
Call:
glm(formula = success ~ numeracy, family = binomial)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.5814 -0.9060 0.3207 0.6652 1.8266
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -6.1414 1.8873 -3.254 0.001138 **
numeracy 0.6243 0.1855 3.366 0.000763 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 68.029 on 49 degrees of freedom
Residual deviance: 50.291 on 48 degrees of freedom
AIC: 54.291
Number of Fisher Scoring iterations: 5
We do the same for anxiety.
model_anxiety <- glm(success ~ anxiety, binomial)
summary(model_anxiety)
Call:
glm(formula = success ~ anxiety, family = binomial)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.8680 -0.3582 0.1159 0.6309 1.5698
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 19.5819 5.6754 3.450 0.000560 ***
anxiety -1.3556 0.3973 -3.412 0.000646 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 68.029 on 49 degrees of freedom
Residual deviance: 36.374 on 48 degrees of freedom
AIC: 40.374
Number of Fisher Scoring iterations: 6
Now we create our plots. First we set up a sequence of length values which we will use to plot the fitted model. Let’s find the range of each variable.
range(numeracy) [1] 6.6 15.7 range(anxiety) [1] 10.1 17.7
Given the range of both numeracy and anxiety. A sequence from 0 to 15 is about right for plotting numeracy, while a range from 10 to 20 is good for plotting anxiety.
xnumeracy <-seq (0, 15, 0.01) ynumeracy <- predict(model_numeracy, list(numeracy=xnumeracy),type="response")
Now we use the predict() function to set up the fitted values. The syntax type = “response” back-transforms from a linear logit model to the original scale of the observed data (i.e. binary).
plot(numeracy, success, pch = 16, xlab = "NUMERACY SCORE", ylab = "ADMISSION") lines(xnumeracy, ynumeracy, col = "red", lwd = 2)
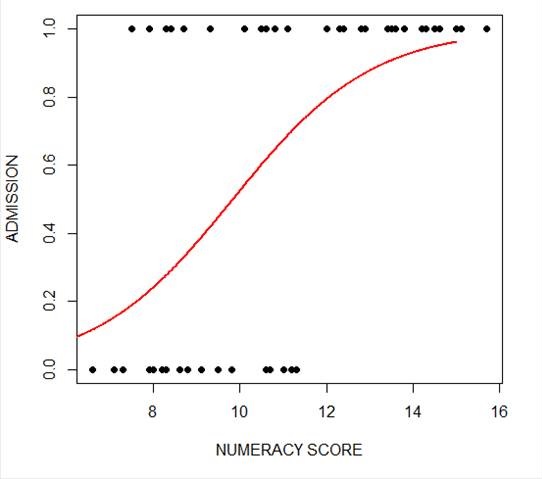The model has produced a curve that indicates the probability that success = 1 to the numeracy score. Clearly, the higher the score, the more likely it is that the student will be accepted.
Now we plot for anxiety.
xanxiety <- seq(10, 20, 0.1) yanxiety <- predict(model_anxiety, list(anxiety=xanxiety),type="response") plot(anxiety, success, pch = 16, xlab = "ANXIETY SCORE", ylab = "SUCCESS") lines(xanxiety, yanxiety, col= "blue", lwd = 2)
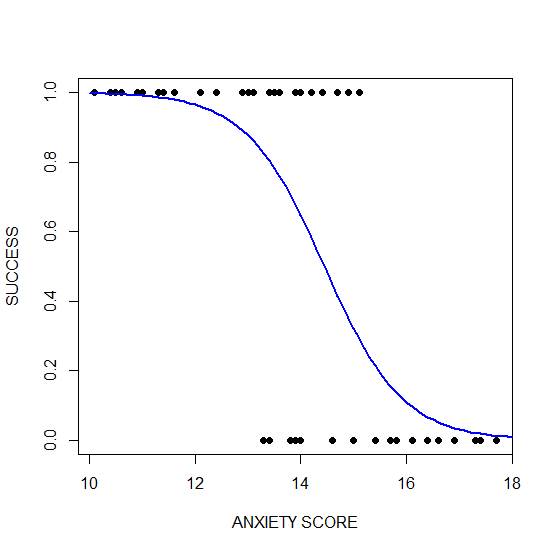Clearly, those who score high on anxiety are unlikely to be admitted, possibly because their admissions test results are affected by their high level of anxiety.
****
See our full R Tutorial Series and other blog posts regarding R programming.
About the Author: David Lillis has taught R to many researchers and statisticians. His company, Sigma Statistics and Research Limited, provides both on-line instruction and face-to-face workshops on R, and coding services in R. David holds a doctorate in applied statistics.
Ordinary Least Squares regression provides linear models of continuous variables. However, much data of interest to statisticians and researchers are not continuous and so other methods must be used to create useful predictive models.
The glm() command is designed to perform generalized linear models (regressions) on binary outcome data, count data, probability data, proportion data and many other data types.
In this blog post, we explore the use of R’s glm() command on one such data type. Let’s take a look at a simple example where we model binary data.