Is it really ok to treat Likert items as continuous? 
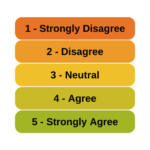And can you just decide to combine Likert items to make a scale? Likert-type data is extremely common—and so are questions like these about how to analyze it appropriately. [Read more…] about Member Training: Analyzing Likert Scale Data
Correlation
Six terms that mean something different statistically and colloquially
by Kim Love and Karen Grace-Martin
Statistics terminology is confusing.
Sometimes different terms are used to mean the same thing, often in different fields of application. Sometimes the same term is used to mean different things. And sometimes very similar terms are used to describe related but distinct statistical concepts.
[Read more…] about Six terms that mean something different statistically and colloquially
Member Training: Confusing Statistical Terms
Learning statistics is difficult enough; throw in some especially confusing terminology and it can feel impossible! There are many ways that statistical language can be confusing.
Some terms mean one thing in the English language, but have another (usually more specific) meaning in statistics. [Read more…] about Member Training: Confusing Statistical Terms
The Difference Between Association and Correlation
What does it mean for two variables to be correlated?
Is that the same or different than if they’re associated or related?
This is the kind of question that can feel silly, but shouldn’t. It’s just a reflection of the confusing terminology used in statistics. In this case, the technical statistical term looks like, but is not exactly the same as, the way we mean it in everyday English. [Read more…] about The Difference Between Association and Correlation
Member Training: Interpretation of Effect Size Statistics
Effect size statistics are required by most journals and committees these days — for good reason.
They communicate just how big the effects are in your statistical results — something p-values can’t do.
But they’re only useful if you can choose the most appropriate one and if you can interpret it.
This can be hard in even simple statistical tests. But once you get into complicated models, it’s a whole new story. [Read more…] about Member Training: Interpretation of Effect Size Statistics
Member Training: Those Darn Ratios!
Ratios are everywhere in statistics—coefficient of variation, hazard ratio, odds ratio, the list goes on. You see them reported in the literature and in your output.
You comment on them in your reports. You even (kinda) understand them. Or, maybe, not quite?
Please join Elaine Eisenbeisz as she presents an overview of the how and why of various ratios we use often in statistical practice.