No, a degree of freedom is not “one foot out the door”!
Definitions are rarely very good at explaining the meaning of something. At least not in statistics. Degrees of freedom: “the number of independent values or quantities which can be assigned to a statistical distribution”.
This is no exception.
We will use Stata’s linear regression output to explain degrees of freedom. Our outcome variable is BMI (body mass index).
The starting point for understanding degrees of freedom is the total number of observations in the model. This model has 303 observations, shown in the top right corner.
But once we use these observations to calculate a parameter estimate the degrees of freedom change.
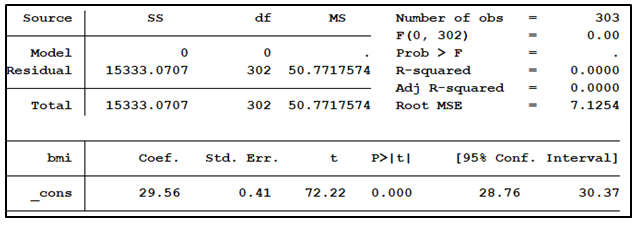
A model run with no predictors, the empty model, provides one estimated parameter value, the intercept (_cons). The intercept in this model is the mean of the outcome variable.
Note that the “Residual” df and the “Total” df are both 302. The empty model has n-1 degrees of freedom, where n = number of observations.
Why does the empty model have n-1 degrees of freedom and not n?
If we know the mean of a series of numbers, there are no restrictions as to the value of those numbers except for one of them.
Why is that? In terms of our outcome variable BMI, if we know the mean, and 302 of the observed values, we know the final subject’s observed BMI value. It is the difference between the mean of BMI times the number of observations and the sum of all other subjects’ BMIs.
There are no restrictions as to how the “other” subjects’ BMI can vary. Knowing the mean of BMI, the final subject’s BMI cannot vary.
Here is the mathematical equation:
In terms of our model above, 302 observations can vary, one cannot. Our empty model has 302 degrees of freedom.
What happens when we include a categorical predictor for body frame which has three categories: small, medium and large?
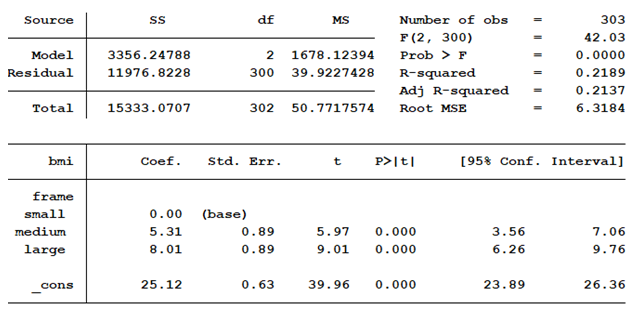
The “Total” number of degrees of freedom remains at n-1, 302. “Model” has been added as a “Source”. Its value for degrees of freedom is 2. Why?
Because we’ve added two new parameter estimates to the model—the regression coefficients for medium and large. The intercept (_cons) represents the mean value of BMI for the reference group, small frame. Medium frame is estimated to be 5.31 greater than small frame, 30.43. Large frame is estimated to be 8.01 greater than small frame, 33.13.
How do these estimates impact the degrees of freedom?
We use the same mathematical logic here as we did for the empty model.
If we know the mean of BMI for small frame, all but one small frame individual’s observed value can vary.
If we know the mean of BMI for medium frame, all but one medium frame individual’s observed value can vary.
If we know the mean of BMI for large frame, all but one large frame individual’s observed value can vary.
We know the “Total” degrees of freedom equal n-1 as a result of calculating the intercept (mean for small frame individuals). One medium frame observation is no longer free to vary since we know the mean BMI for medium frame observations. The same is true for large frame individuals.
Our model has used a total of 2 degrees of freedom for the additional two mean values estimated. That is why “Model” has 2 df. The residual df represents the number of observations whose BMI can still vary. To calculate the residual’s df we simply subtract the “Model” df from the “Total” df.
Each time we add predictors to the model we add parameters, so are increasing the “Model” df. If the predictor is continuous, we are adding one df to the “Model” df. If the predictor is categorical, we are adding the number of categories minus one.
