When you need to compare a numeric outcome for two groups, what analysis do you think of first? Chances are, it’s the independent samples t-test. But that’s not the only, or always, the best option. In many situations, the Mann-Whitney U test is a better option.
The non-parametric Mann-Whitney U test is also called the Mann-Whitney-Wilcoxon test, or the Wilcoxon rank sum test. Non-parametric means that the hypothesis it’s testing is not about the parameter of a particular distribution.
It is part of a subgroup of non-parametric tests that are rank based. That means that the specific values of the outcomes are not important, only their order. In other words, we will be ranking the outcomes.
Like the t-test, this analysis tests whether two independent groups have similar typical outcomes. You can use it with numeric data, but unlike the t-test, it also works with ordinal data. Like the t-test, it is designed for comparisons, and not for estimation or prediction.
The biggest difference from the t-test is that it does not compare means. The Mann-Whitney U test determines whether a random observation from one group tends to be higher (or lower) than a random observation from the other group. Imagine choosing two observations, one from each group, over and over again. This test will determine whether one group is more likely to have the higher values.
It has many advantages: It is a straightforward comparison of means. There are versions for similar and different variances in the two groups. Many people are familiar with it.
Why not the t-test?
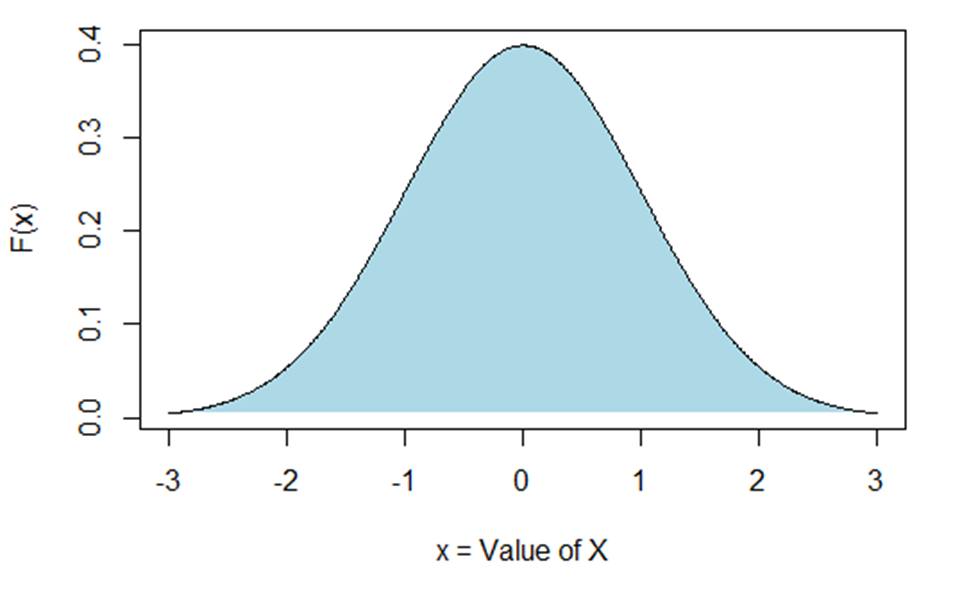
There is only one real disadvantage to a t-test— both groups must have a normal distribution. That is, if you make a
histogram of the outcome for either group, it should resemble the figure below.
There are multiple ways in which a distribution can be non-normal. A few common ones include:
- The observations are skewed (values are concentrated on one end of the range)
- There are outliers (one or two observations that are high or low enough to be separate from the others)
- The outcomes are not approximately continuous (limited possible values)
Assumptions
Sometimes people believe that non-parametric tests have no assumptions. That’s not true, but the assumptions are relaxed relative to many parametric tests. Three assumptions for the Mann-Whitney U test are:
- Both samples are random samples from their respective populations.
- There is independence within each sample, and between the two samples.
- The measurement scale is at least ordinal.
How it Works
Most popular statistical software will perform the Mann-Whitney U test. There are four steps:
1. Order outcomes within each group.
2. Rank the outcomes overall, keeping track of which group they belong to.
3. Calculate a test statistic. There are several versions, but one is:
where T is the sum of the overall ranks from just one group, and n₁ is the sample size for that group.
4. Determine a p-value. There are charts available for this. U also has a known mean and standard deviation, which is often
used to calculate a Z statistic .
When Not to Use It
Finally, it is not always appropriate to use the Mann-Whitney U test instead of the paired t-test. Do not use it if:
- The observations within each group are not independent.
- The observations in the two groups are paired or otherwise related.
- The outcomes are nominal (non-ordered categories).
You can use it, but other tests are likely more powerful if:
- The outcomes are normally distributed (use the independent t-test).
- You can transform the outcomes to be normally distributed (consider the independent t-test). The outcomes have another distribution (e.g., Poisson or multinomial) that can use other parametric methods.
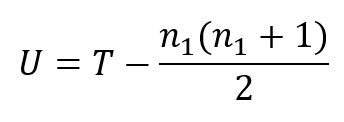
Leave a Reply