Interpreting Regression Coefficients in Models other than Ordinary Linear Regression

Someone who registered for my upcoming Interpreting (Even Tricky) Regression Models workshop asked if the content applies to logistic regression as well.

The short answer: Yes

The long-winded detailed explanation of why this is true and the one caveat:

One of the greatest things about regression models is that they all have the same set up:

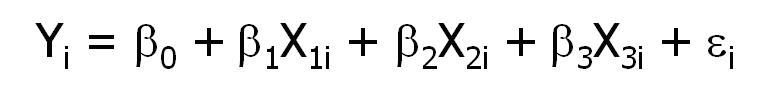
The left hand side is the response, Y.  It gets an i subscript because each individual has its own value of Y.

The Xs are the predictor variables.  And the βs, the coefficients, tell you about how each X relates to Y, in the context of the presence of the other predictors.  This is the part we really want to find out.

The residuals, ε, are the part of Y that doesn’t relate to the Xs.  They’re important to the model because if we misrepresent how they behave, it means we are also misrepresenting the βs.  But as long as we get a picture of their behavior right, we can make good inferences about how Y relates to the Xs.

So this is the actual model for an ordinary least squares linear regression.  The left hand side of the equation is just Y and ε, the error term, has a normal distribution.

Learn how to best approach coefficients that are often times tricky to interpret.
Free Webinar - Interpreting Linear Regression Coefficients: A Walk Through Output.

For other types of regression models, like logistic regression, Poisson regression, or multilevel models, all the βs and Xs stay the same.  The only parts that can differ:

1. Instead of Y on the left, there can be a function of the mean of Y–a link function.

2. Instead of a normal distribution, Y|X can have another distribution.

So for example, in a logistic regression, the function of Y is a logit (a.k.a. log-odds) function and the distribution of Y|X is binomial.

And in a multilevel model, there is no special transformation of Y, but the residual gets split into two pieces, both of which are normally distributed.

But as I said, the βs and the Xs don’t change.

The interpretation of each coefficient (at least the trickiest parts, which have to do with the Xs) is about two things:

1. the structure of X

2. what other Xs are in the model.

So interpreting coefficients is done the same basic way regardless of how Y and ε behave.  And that’s what we cover in the majority of the workshop–centering, dummy variables, interactions, correlated predictors, etc.

The one caveat:

But logistic regression also involves that link function on the mean of Y, so there is an extra step involved in interpreting logistic regression coefficients.  So you still need to understand the centering, dummy variables, etc., but you need to understand the logit link function as well.

This is slightly different from doing a transformation of Y, which is usually done to correct non-constant variance or skewed residuals.

I had not planned to, but will briefly add interpreting transformed Y’s and link functions into the workshop.

And if you want more information about the transformation and what it does to all types of logistic regression coefficients, I did a webinar last year on  logistic regression.  You can watch the webinar here.

So you still need to understand dummy variables, centering, correlated predictors, and all that tricky stuff to interpret the odds ratios.  Which is why I recommend learning the tricky stuff in the context of the (relatively) simple linear model before tackling more complicated models.

Tagged as: Count models, interpreting regression coefficients, Logistic Regression