A well-fitting regression model results in predicted values close to the observed data values. The mean model, which uses the mean for every predicted value, generally would be used if there were no useful predictor variables. The fit of a proposed regression model should therefore be better than the fit of the mean model. But how do you measure that model fit?
Mixed and Multilevel Models
Beyond R-squared: Assessing the Fit of Regression Models
February 20th, 2024 by Karen Grace-Martin
When the Hessian Matrix Goes Wacky
December 20th, 2023 by Karen Grace-Martin
If you have run mixed models much at all, you have undoubtedly been haunted by some version of this very obtuse warning: “The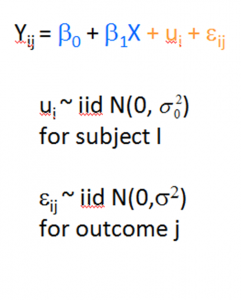 
Hessian (or G or D) Matrix is not positive definite. Convergence has stopped.”
Or “The Model has not Converged. Parameter Estimates from the last iteration are displayed.”
What on earth does that mean?
Let’s start with some background. If you’ve never taken matrix algebra, (more…)
The Difference Between Crossed and Nested Factors
December 18th, 2023 by Karen Grace-Martin
One of those tricky, but necessary, concepts in statistics is the difference between crossed and nested factors.
As a reminder, a factor is any categorical independent variable. In experiments, or any randomized designs, these factors are often manipulated. Experimental manipulations (like Treatment vs. Control) are factors.
Observational categorical predictors, such as gender, time point, poverty status, etc., are also factors. Whether the factor is observational or manipulated won’t affect the analysis, but it will affect the conclusions you draw from the results.
The Wide and Long Data Format for Repeated Measures Data
December 2nd, 2023 by Karen Grace-Martin
One issue in data analysis that feels like it should be obvious, but often isn’t, is setting up your data.
The kinds of issues involved include:
- What is a variable?
- What is a unit of observation?
- Which data should go in each row of the data matrix?
Answering these practical questions is one of those skills that comes with experience, especially in complicated data sets.
Even so, it’s extremely important. If the data isn’t set up right, the software won’t be able to run any of your analyses.
And in many data situations, you will need to set up the data different ways for different parts of the analyses. (more…)
Concepts in Linear Regression to know before learning Multilevel Models
November 21st, 2023 by Karen Grace-Martin
Are you learning Multilevel Models? Do you feel ready? Or in over your head?
It’s a very common analysis to need to use. I have to say, learning it is not so easy on your own. The concepts of random effects are hard to wrap your head around and there is a ton of new vocabulary and notation. Sadly, this vocabulary and notation is not consistent across articles, books, and software, so you end up having to do a lot of translating.
Mixed Models with Crossed Random Factors
October 23rd, 2023 by Karen Grace-Martin
When you hear about multilevel models or mixed models, you very often think of a nested design. Level 1 units 
nested in Level 2 units, which are in turn possibly nested in Level 3 units. But these variables that define the units and that become random factors in the model can, in fact, be crossed with each other, not nested.