One approach to model building is to use all predictors that make theoretical sense in the first model. For example, a first model for determining birth weight could include mother’s age, education, marital status, race, weight gain during pregnancy and gestation period.
The main effects of this model show that a mother’s education level and marital status are insignificant.
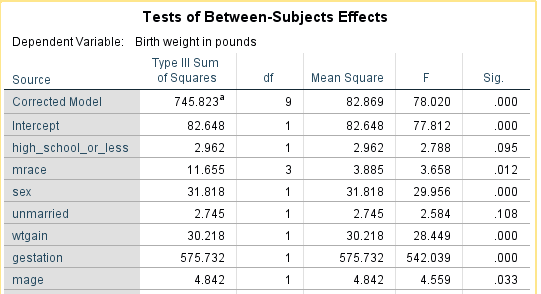
Dropping marital status and running a new model we find that the mother’s education is now significant. We also see an improvement in the significance of the mother’s age from p=0.033 to p=0.004.
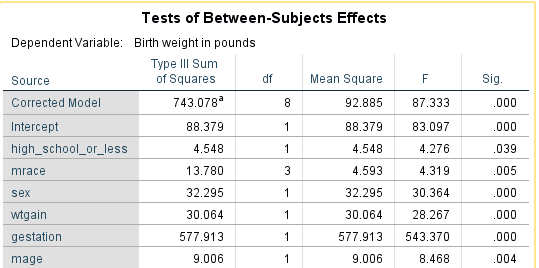
What if mother’s education level was dropped instead of marital status?
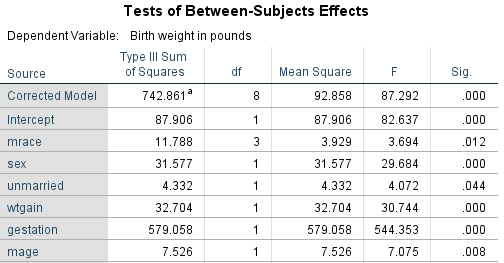
Marital status is now significant. Mother’s age has a lower p-value as well when compared to the model using both education and marital status. Why is there a conflict between the three models? Why the improvement with the statistical significance of mother’s age?
Examining a cross tabulation shows us the two predictors are not duplicates. If they were duplicates we would have zero counts in the bottom left and upper right cells. If one variable was the reverse code of the other variable the cells in the upper left and bottom right would have zero counts.
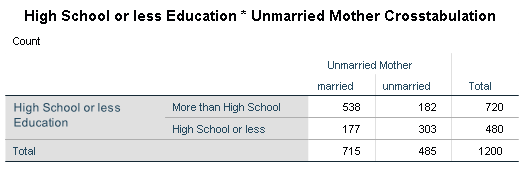
Perhaps the two predictors are providing the same information about birth weight. The tables below examine the mean birth weight per category for each predictor. The mean birth weights are almost identical for the two predictors.
The mean age for the two predictors is almost identical as well.
The summary statistics for this data shows the same mean birth weight for babies born to mothers with more than a high school education is the same as the mean birth weight for married mothers. The same is true when comparing unmarried mothers to mothers with no post-high school education.
Does theory suggest these relationships exist? If they run counter to theory the researcher should explain the conflicts found within the data.
Running a series of descriptive statistics before running models can help identify issues such as these shown here. Otherwise, we might reach inaccurate conclusions due to an unusual sample.
Jeff Meyer is a statistical consultant with The Analysis Factor, a stats mentor for Statistically Speaking membership, and a workshop instructor. Read more about Jeff here.
