by Maike Rahn, PhD
One of the hardest things to determine when conducting a factor analysis is how many factors to settle on. Statistical programs provide a number of criteria to help with the selection.
Eigenvalue > 1
Programs usually have a default cut-off for the number of generated factors, such as all factors with an eigenvalue of ≥1.
This is because a factor with an eigenvalue of 1 accounts for as much variance as a single variable, and the logic is that only factors that explain at least the same amount of variance as a single variable is worth keeping.
But often a cut-off of 1 results in more factors than the user bargained for or leaving out a theoretically important factor whose eigenvalue is just below 1. So use this criterion only with extreme caution.
Scree Plot
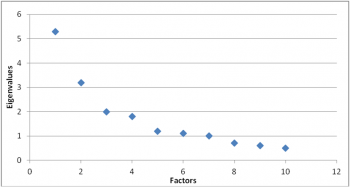
Another option is the scree plot. A scree plot shows the eigenvalues on the y-axis and the number of factors on the x-axis. It always displays a downward curve.
The point where the slope of the curve is clearly leveling off (the “elbow) indicates the number of factors that should be generated by the analysis.
Unfortunately, both criteria sometimes yield an unreasonably high number of factors. In the above example, a cut-off of an eigenvalue ≥1 would give you seven factors. And the scree plot suggests either three or five factors due to the way the slope levels off twice.
It is important to keep in mind that one of the reasons for running a factor analysis is to reduce the large number of variables that describe a complex concept such as socioeconomic status to a few interpretable latent variables (=factor). In other words, we would like to find a smaller number of interpretable factors that explain the maximum amount variability in the data.
Total Percent Variance Explained
Therefore, another important metric to keep in mind is the total amount of variability of the original variables explained by each factor solution.
Remember that every factor analysis has the same number of factors as it does variables, and those factors are listed in the order of the variance they explain. You’ll always be able to explore more total variance by keeping more factors in the solution, but later factors explain so little variation, they don’t add much.
If the first three factors together explain most of the variability in the original 10 variables, then those factors are clearly a good, simpler substitute for all 10 variables. You can drop the rest without losing much of the original variability.
But if it takes 7 factors to explain most of the variance in those 10 variables, you might as well just use the original 10.
Meaningful Factors
It is also important that the rotated factors make theoretical sense to the researcher.
Do the variables that are loading on the same factor make sense together? If you can name the concept they represent, that’s indicative that the factor solution is a reasonable one.
Likewise, do the variables that are loading on different factors measure something different? If you’ve created a scale with two items that are just different wordings of the same underlying question, a factor solution that puts them on different factors doesn’t make a lot of sense.
Keep in mind that each of the identified factors should have at least three variables with high factor loadings, and that each variable should load highly on only one factor.
After looking at the scree plot as a guide, I often wind up forcing my analysis to run between one and five factors, and then develop the five models separately.
Usually it quickly becomes clear when to drop a factor solution, especially when one factor has only two important variables and therefore does not explain much of the overall variability, or if it is not very convincing based on my theoretical expectations.
About the Author: Maike Rahn is a health scientist with a strong background in data analysis. Maike has a Ph.D. in Nutrition from Cornell University.


Do we select factors to retain after rotation or before?
Hey, I want to ask you about the scree plot a little more… If a scree graph is given then how should you interpret it? Thank you!
Dear Chanpreet Sandhu
The value of the determinant should be greater than 0.00001.
Anything less suggest high degree of multicollinearity which implies that there are variables with high coefficient correlation with other variables. You need to delete some of these variables from the model and ensure the determinant is higher than 0.00001 (that’s four zeros after decimal). Look at the correlation matrix to spot high correlation coefficient values of more than 0.9
can i ask a question?
how about when on your original questionnaire, after factor analysis, there came to be new 5 factors.
In what order would the questions be?
A. follow the new five factors
B. Random Selection
C. Author’s Prerogative
THANK YOU!
Arrange the factors in the order of highest percentage of variance to lowest.
Hi,
Thanks for sharing the knowledge.
If I want to cite, what should I write?
Thanks.
God bless
Thanks, I really found this write-up very helpful. I am about to conduct Factor Analysis to establish the construct validity of my data collection instruments. So, this article has widen my horizons on factor analysis. Thanks a lot.
Hi,
I am a little bit confused about factor analysis. I would like to ask some questions.
1) Is scree plot and eigenvalue is the only crieterion? because these two can give us more factors like 10 and we want 3 or 4.
2) Can we run fixed factor on spss option instead of eigenvalue? Because the results of fixed factors are some time good than the above. If we use this fixed factor option in spss, how we can can explain and give reference for it?
Hi Ijaz,
No, there are many possible criteria and the eigenvalue > 1 criteria isn’t a great one.
when i create my factor analysis, for correlation matrix my determinant =3.7853-6, i know this number should be greater than 0.001 but i have no clue what this number means.
if you could explain this it would be greatly helpful, thank you!
Hello,
As I am going through all this, I am still mystified by a few things:
1. When looking at correlation matricies, and the eigenvalues are determined, to me there is no clear “assignment” of which eigenvalue goes to which variable. If there’s a 3 x 3 correlation matrix and there happens to be 3 eigenvalues, how do you know which eigenvalue is for which variable? (May seem like a stupid question, sorry. I’ve looked in a lot of places on the internet and there is no real clear explanation.)
2. I understand the math when it comes to determining eigenvalues from a correlation matrix. What I don’t get is how once these factors are chosen based on the value of the eigenvalue, how these factor loading tables are created. I understand they are a type of correlation, but how are these numbers generated? If there’s just a good resource to link to, that will work for me.
Thank you in advance.
Thanks u so much for your contribution of knowledge towards factor analysis, it has been a very good explanation, clear and concise. Though am very new to the topic, I still need more exposition in regards the topic how and when to use it, majorly the interpretation of the screen plot and the uses. Thanks.
Hi Maike,I am appreciating your contribution for this.I am too new to this field and carrying out one research on job satisfaction where i have used various factors affecting job satisfaction. 21 questions has been framed to carry out the survey. Those questions were basically on various factors like pay, perks and benefits, administrative policies etc. 1. So can i consider those questions as different factors for factors analysis?2.Is factor analysis is useful in reducing those 21 questions (factors) in small number of question (factors)?3. Is there any criteria to feed factors sequentially (according to high loading)?Please help me on thsese questions?
Dear Mike,
I have a problem here. when it is suggested that ‘…each variable should load highly on only one factor’ what is the benchmark of this high loading. I had extracted three factors and one variable load in first second and third factor in this order 0.745; 0.231 and 0.68; is is it reasonable to suggest that it load relatively highly on first factor
Thanks
John
Hi John,
There isn’t a consensus about high loading, but .4 is a common cutoff.
Dear Maike
I really do appreciate you for your contribution towards spreading knowledge for the people around the world.
Thanks
Regards
FARAZ
Dear Friedrich,
I am glad you are bringing up the question whether we decide the number of retained factors with the scree plot by coming from the left or the right. There are indeed different approaches to factor retention with scree plots, and they are based on how researchers were trained.
Your suggestion to run the factor analysis with a range of solutions for the suggested number of retained factors is exactly right.
In an exploratory factor analysis, the decision of how many factors to extract should be based on your interpretation of the underlying relationships of your variables with the latent factor. In other words, a 4 factor solution may explain more of the overall variability, but it may not generate 4 factors that make the most sense theoretically. Looking for solutions that generate less (or more) factors than suggested in the scree plot is always a good approach.
In terms of the decision of the number of factors based on the scree plot: the change in slope (or in your words elbow-criteria) is what determines how many factors you use. I usually come from the left. So if the slope of the line changes between 3 and 4, then I would consider three factors. I would probably ultimately test 2 to 6 solutions while trying to select one with fewer retained factors, since the scree plot was not all that clear to begin with.
Best wishes,
Maike
Hello Karen and Maike,
I greatly enjoyed reading your clear explanations of Factor Analysis. Very helpful, particularly for those new to the idea.
Best wishes,
David
Dear Maike,
“And the scree plot suggests either three or five factors due to the way the slope levels off twice.”
i would have said, yes and no concerning the elbow-criteria. but i would extract either 2 or 4, because those points hover over the interpolation line coming from the RIGHT…
what do you reckon?
best,
fritz