Most of the time when we plan a sample size for a data set, it’s based on obtaining reasonable statistical power for a key analysis of that data set. These power calculations figure out how big a sample you need so that a certain width of a confidence interval or p-value will coincide with a scientifically meaningful effect size.
But that’s not the only issue in sample size, and not every statistical analysis uses p-values.
One example is Factor Analysis.*
A factor analysis is a measurement model of an underlying construct. So like regression models, structural equation models, and latent class models, the focus in on understanding the structure of the relationships among variables.
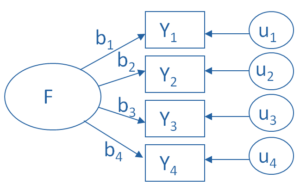The specific focus in factor analysis is understanding which variables are associated with which latent constructs. The approach is slightly different if you’re running an exploratory or a confirmatory model, but this overall focus is the same.
If power isn’t the main issue, how big of a sample do you need in factor analysis?
The short answer is: a big one.
The long answer is a little more complicated, mainly because there isn’t one right answer. Authors have differing opinions on exactly how many subjects you need, and on exactly which criterion to use.
Rules of Thumb
For example, some authors use a criterion based on the total sample size:
— 100 subjects=sufficient if clear structure; more is better (Kline, 1994)
— 100 subjects=poor; 300 =good; 1000+ = excellent (Comrey & Lee, 1992)
— 300 subjects, though fewer works if correlations are high among variables (Tabachnik & Fidell, 2001)
Others base it on a ratio of the number of cases to the number of variables involved in the factor analysis:
— 10-15 subjects per variable (Pett, Lackey, & Sullivan)
— 10 subjects per variable (Nunnally, 1978)
— 5 subjects per variable or 100 subjects, whichever is larger (Hatcher, 1994)
— 2 subjects per variable (Kline, 1994)
And then others base it on a ratio of cases to the number of factors:
20 subjects per factor (Arrindel & van der Ende, 1985).
Rules of Thumb are not Rules
But the reality is these are rules of thumb, not rules. More recent simulation studies have found that the required sample size depends on a number of issues in the data and in the model, working together. They include all the issues listed above and a few more.
Here are a few takeaways:
1. You’re going to need a large sample. That means in the hundreds of cases. More is better.
2. You can get away with fewer observations if the data are well-behaved. If there are no missing data and each variable highly loads on a single factor and not others, you won’t need as many cases. But counting on the data behaving is like counting on the weather behaving during hurricane season. You’ll have a better outcome most of the time if you plan for the worst.
3. The main issue with small data sets is overfitting (a secondary issue is if the sample is really small, the model won’t even converge). It’s a simple concept: when a sample is too small, you can get what looks like good results, but you can’t replicate those results in another sample from the same population.
All the parameter estimates are so customized to this particular sample, that they’re not useful for any other sample. This can, and does, happen in any model, not just factor analysis.
*Yes, Confirmatory Factor Analysis can use p-values, for overall model fit chi-square tests as well as specific path coefficients. Exploratory Factor Analysis does not.
Wolf, E., K. Harrington S. Clark, and M. Miller (2013). Sample Size Requirements for Structural Equation Models: An Evaluation of Power, Bias, and Solution Propriety, Educ Psychol Meas. 2013 December ; 76(6): 913–934.
Costello, A. and Osborne, J. (2005). Exploratory Factor Analysis: Four recommendations for getting the most from your analysis. Practical Assessment, Research, and Evaluation, 10(7), 1-9.
Helpful resources for a Ph.D. student indeed! Thank you!