If you have count data you use a Poisson model for the analysis, right?
The key criterion for using a Poisson model is after accounting for the effect of predictors, the mean must equal the variance. If the mean doesn’t equal the variance then all we have to do is transform the data or tweak the model, correct?
Let’s see how we can do this with some real data. A survey was done in Australia during the peak of the flu season. The outcome variable is the total number of times people asked for medical advice from any source over a two-week period.
We are trying to determine what influences people with flu symptoms to seek medical advice. The mean number of times was 0.516 times and the variance 1.79.
The mean does not equal the variance even after accounting for the model’s predictors.
Here are the results for this model:

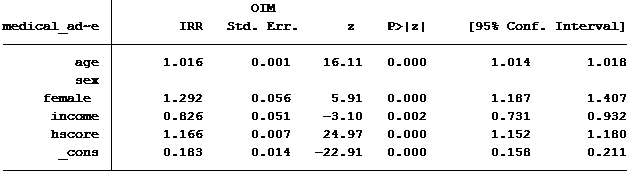
Running the analysis, we find our model generated a Pearson Chi2 dispersion statistic of 2.924. If the variance equals the mean this dispersion statistic should approximate 1.
Running an overdispersed Poisson model will generate understated standard errors. Understated standard errors can lead to erroneous conclusions.
A number of excellent text books provide methods of eliminating or reducing the overdispersion of the data. One of the methods is known as “scaling the standard errors”. The model weight is replaced with “the inverse square root of the dispersion statistic”.
How this works is: the model is run, the dispersion statistic is calculated and then the model standard errors are multiplied by the square root of the dispersion.
Back in the good old days before computers you had to do all this by hand. Today most statistical software packages will do this for you. You just have to write the syntax correctly. Here are the results when we adjust the standard errors by the dispersion statistic.
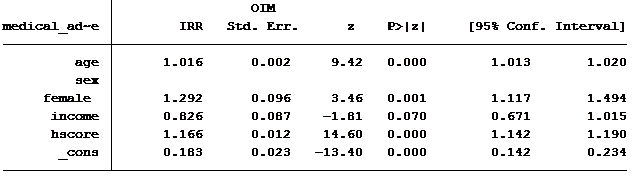
Notice that the coefficients are identical but the standard errors are larger for the scaled version, which is what we want.
But does correcting for our overdispersion in this manner mean that we should use the scaled Poisson model?
There are other methods we could choose from: “quasi-likelihood” model, sandwich or robust variance estimators or bootstrapped standard errors.
Seldom would all methods generate the same results.
My suggestion: rather than use an ad-hoc method to make a model work that doesn’t quite fit, use the count model that best fits the data.
Graphing can be an excellent way to see how a model fits the data. Phil Ender at UCLA created a third party add-on for Stata users called nbvargr. Joseph Hilbe in his book “Modeling Count Data” provides the code (syntax) to generate similar graphs in Stata, R and SAS.
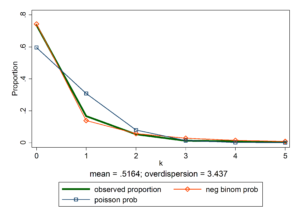
You can see from the graph that the negative binomial probability curve fits the data better than the Poisson probability curve.
Here is the output using a negative binomial model.
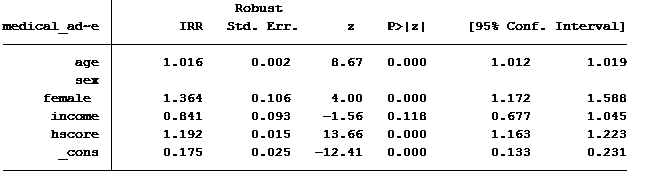
Please note that there are a few quantitative methods for determine the best model for the data as well. These should be used as well when determining which model fits the data best.
Jeff Meyer is a statistical consultant with The Analysis Factor, a stats mentor for Statistically Speaking membership, and a workshop instructor. Read more about Jeff here.


Hi, by “quantitative methods for determining the best model for the data “, did you refer to BIC or AIC to find out best model fit for data. Can you kindly elaborate on this a little bit. Thanks
There is no one best choice between AIC and BIC. BIC penalizes you more for additional predictors as compared to AIC. You might want to run a likelihood ratio test to help you decide which model to use, assuming your model comparisons are nested.