Imagine this scenario:
This year’s flu strain is very vigorous. The number of people checking in at hospitals is rapidly increasing. Hospitals are desperate to know if they have enough beds to handle those who need their help.
You have been asked to analyze a previous year’s hospitalization length of stay by people with the flu who had been admitted to the hospital. The predictors in your data set are age group, gender and race of those admitted. You also have an indicator that signifies whether the hospital was privately or publicly run.
You use a linear regression to regress your outcome variable, number of days spent in the hospital, on the predictors mentioned above. Your game plan is to use histograms to show hospital administrators the predicted length of stay based on different demographics. They can then use the predicted responses to match the client who they serve.
You start by first graphing the length of stay by private and public hospitals.
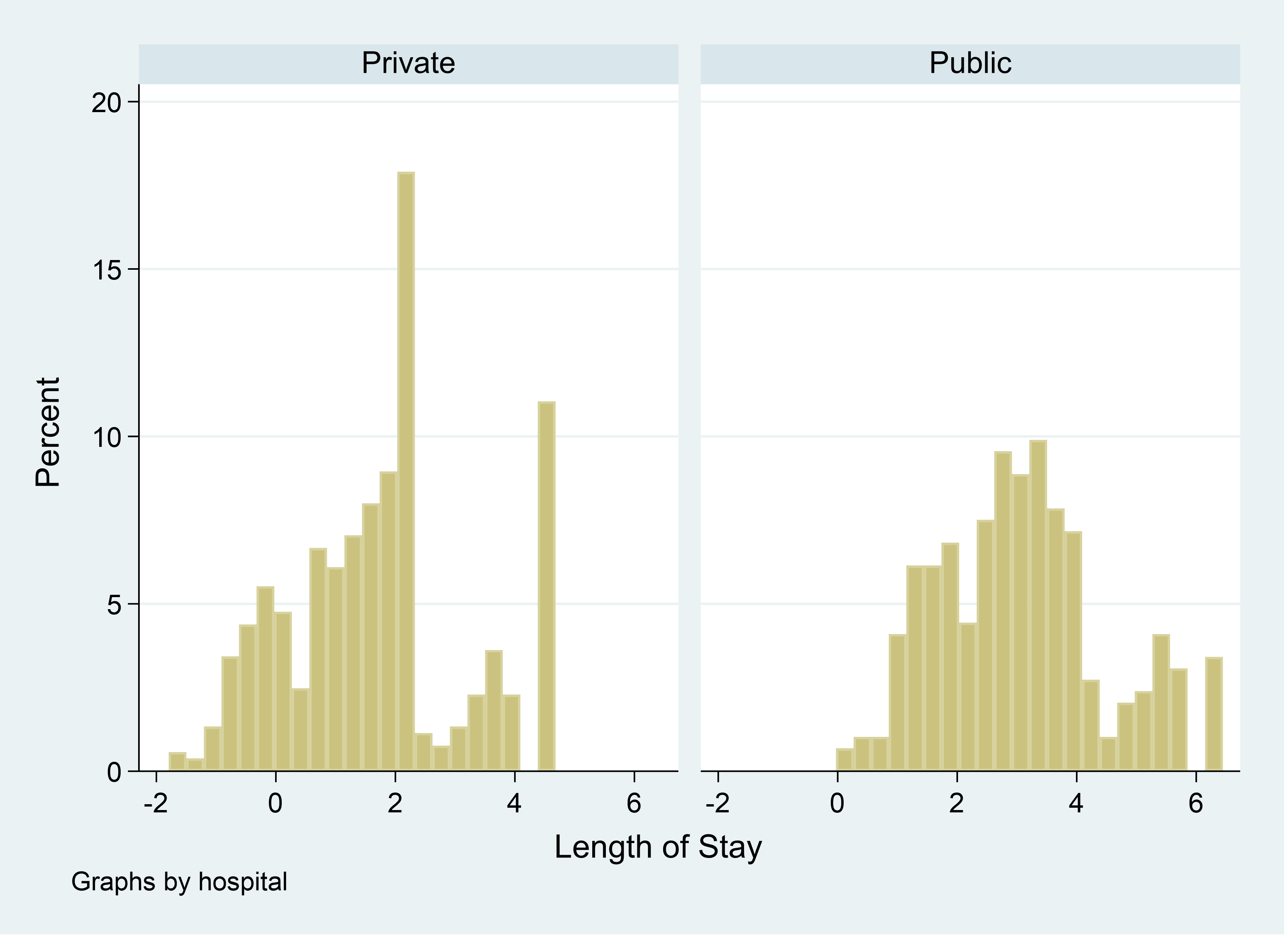
You notice that there are people with a negative length of stay in private hospitals. So you ask a colleague how to explain that!
She points out that your outcome is the count of the number of days hospitalized. Therefore you need to use either a Poisson or negative binomial count model.
You then rerun the model using a negative binomial model. Your graph now looks a lot better.
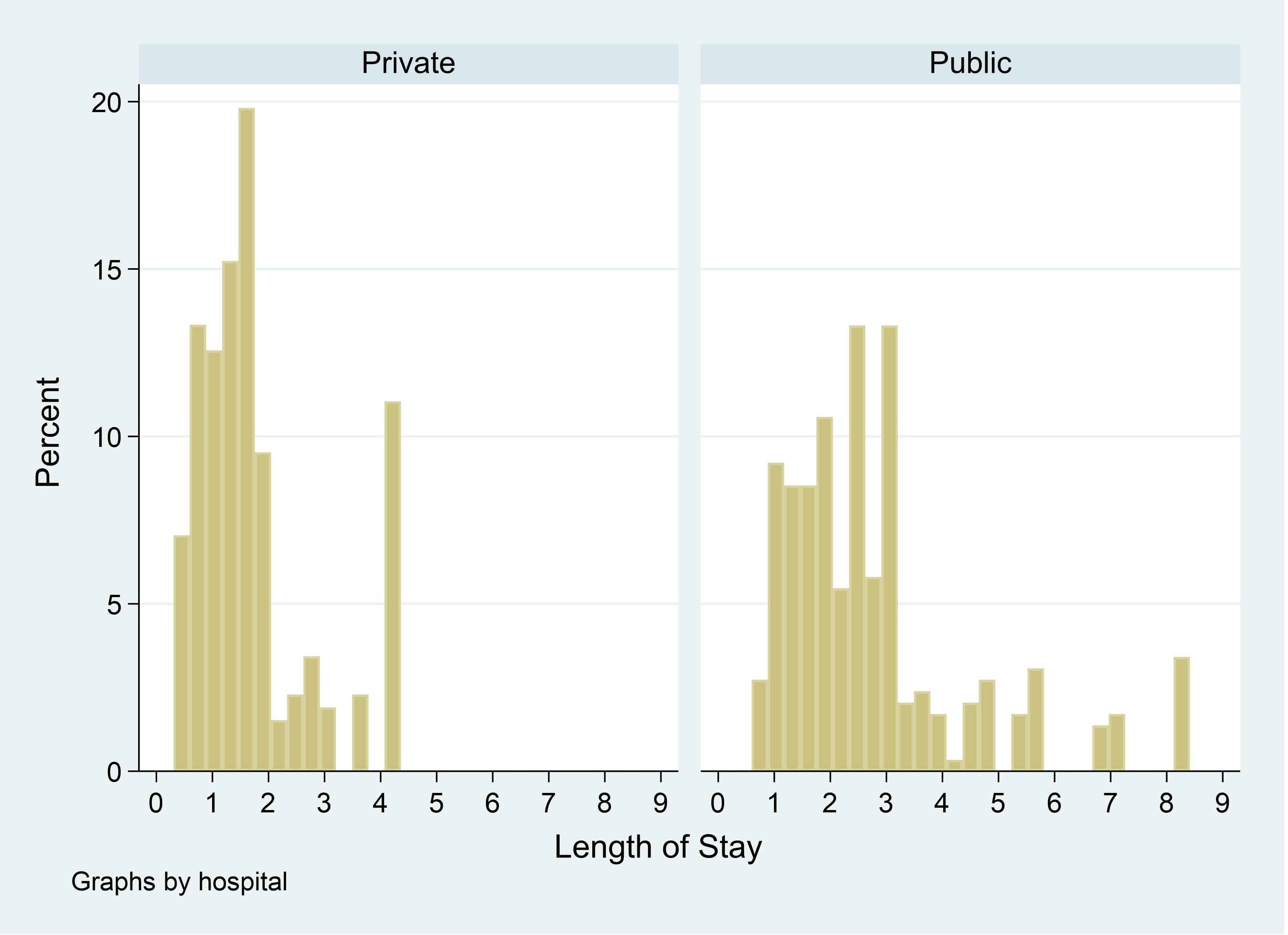
Interestingly the length of stay is longer in a public hospital. But you also notice there are a fair number of people who stayed less than a full day in the private hospitals. This can’t be true because the minimum length of stay is 1 day. Your data shows the minimum length of stay is one day.
How can this problem be solved? You need to use a truncated count model. A truncated model allows you to set the minimum count. In this case it is 1. Here is the histogram using a truncated negative binomial count model.
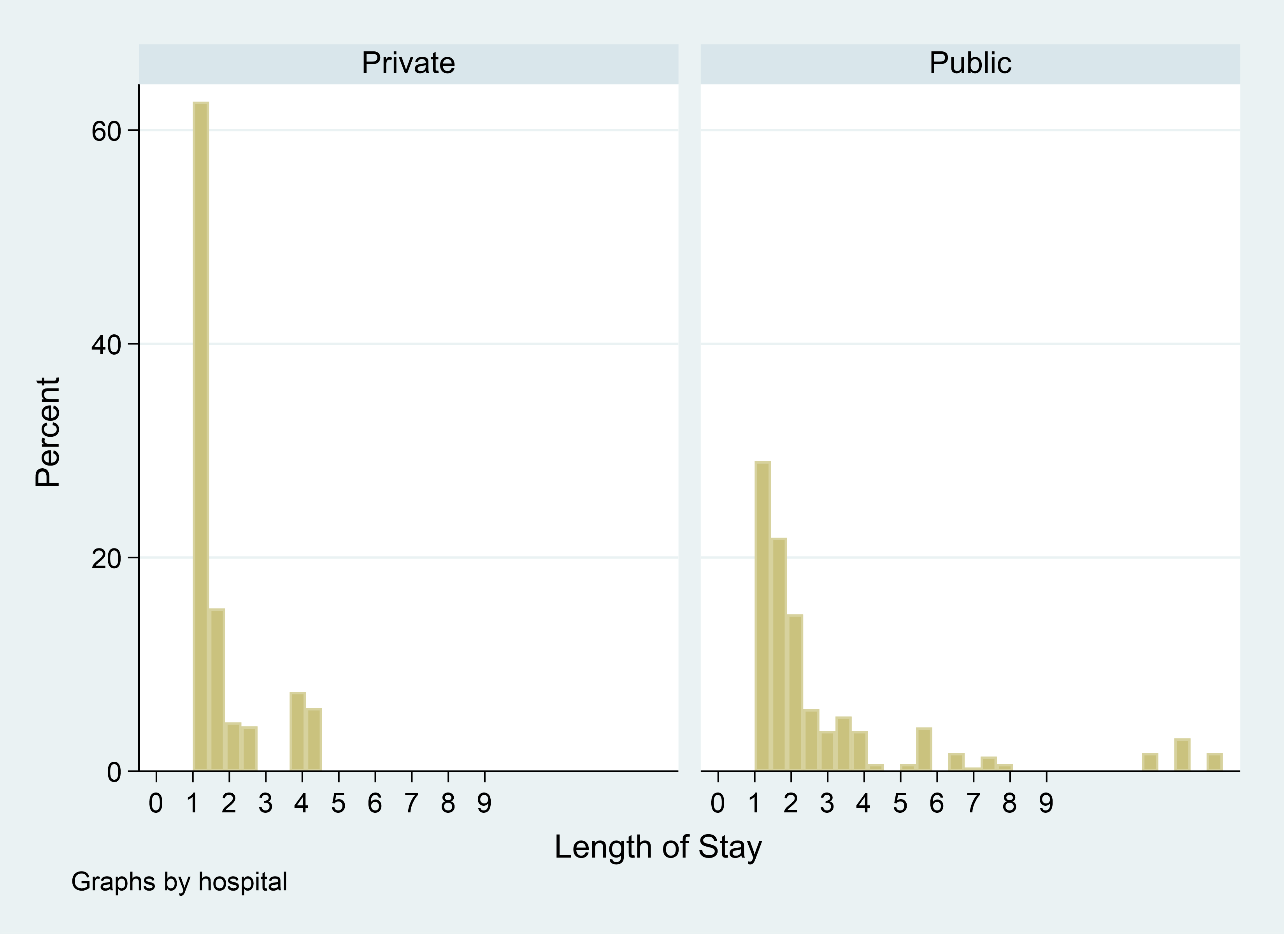
From here you can now start controlling for various demographic factors. You may wonder why the predicted values aren’t all whole numbers. We will look at that in the next article.
Jeff Meyer is a statistical consultant with The Analysis Factor, a stats mentor for Statistically Speaking membership, and a workshop instructor. Read more about Jeff here.


I’m not sure “your outcome is the count of the number of days hospitalized” answers the question of why there are negatives. A more clear explanation of this being predicted values from the regression could be helpful.
Also for clarity, truncated means that those values less than 1 are assigned to one, rather than excluded.