Removing the Intercept from a Regression Model When X Is Continuous

In a recent article, we reviewed the impact of removing the intercept from a regression model when the predictor variable is categorical. This month we’re going to talk about removing the intercept when the predictor variable is continuous.

Spoiler alert: You should never remove the intercept when a predictor variable is continuous.

Here’s why.

Let’s go back to the cars we talked about earlier. Using the same data, if we regress weight on the continuous variable length (in inches) and include the intercept (labeled _cons), we get the following results:

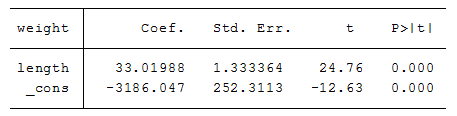
If we exclude the intercept, we get this:

Notice the slope of length has dropped from 33 to 16. It’s the estimate of the relationship between length and weight of the cars we’re interested in and we’ve biased it. Not good.

There’s another problem: residuals.

The table below is a summary of the residuals with (labelled wc) and without (nc) the intercept.

The standard deviation of the residuals from the without-intercept model will never be as low as those from the with-intercept model. Remember, residual variance is unexplained and we want to minimize it.

Additionally, the mean of the residuals will not equal zero, which is a requirement for an OLS model.

Why all these problems?

When you eliminate an intercept from a regression model, it doesn’t go away. All lines have intercepts. Sure, it’s not on your output. But it still exists.

Instead you’re telling your software that rather than estimate it from the data, assign it a value of 0.

Let’s just repeat that for emphasis:

When you remove an intercept from a regression model, you’re setting it equal to 0 rather than estimating it from the data.

The graph below shows what happens.

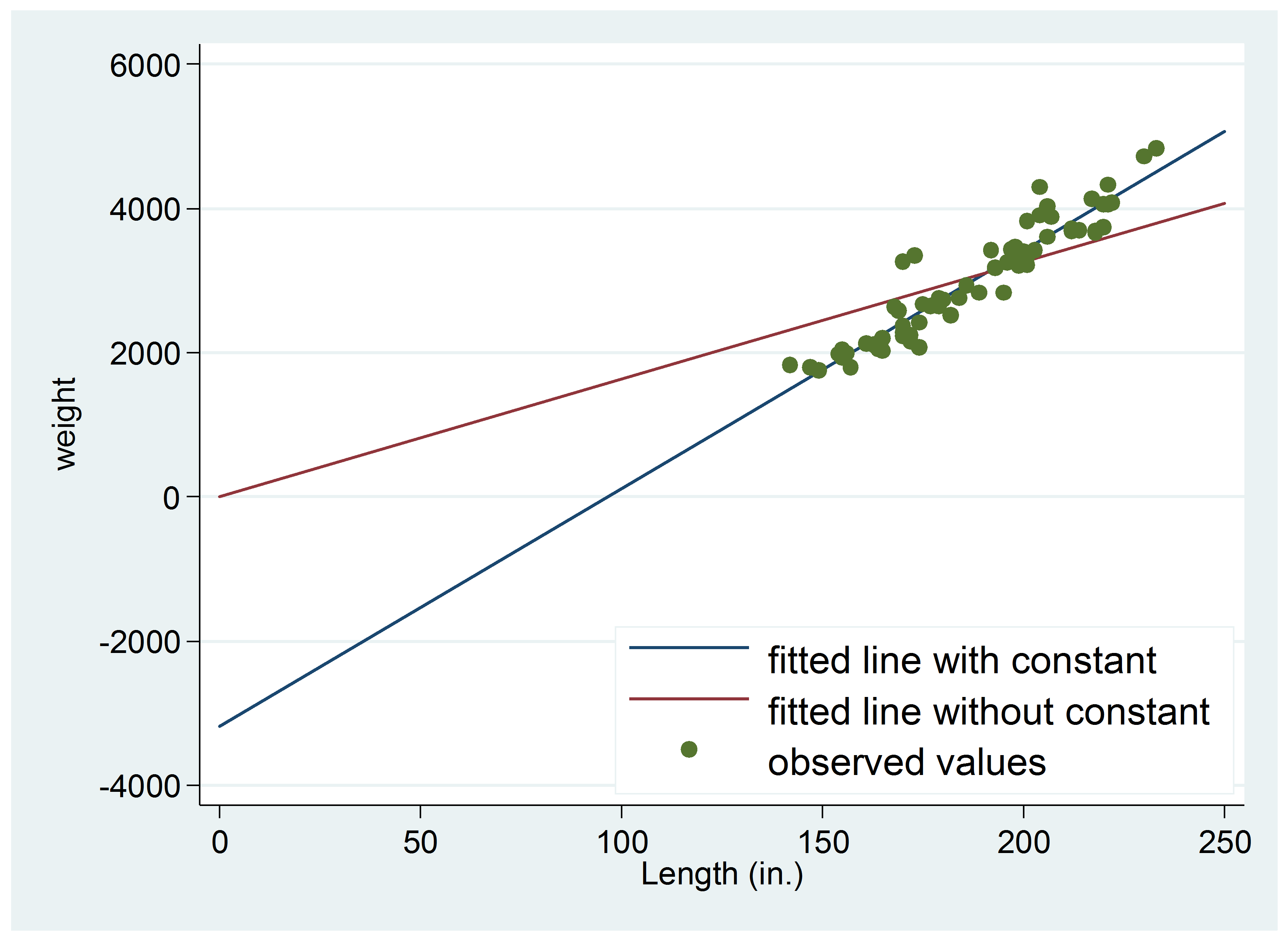
The fitted line of the model estimated the intercept passes through most of the actual data while the fitted line for the unestimated intercept model does not.

Forcing the intercept to equal 0 forces the line through the origin, which will never fit as well as a line whose intercept is estimated from the data.

Jeff Meyer is a statistical consultant with The Analysis Factor, a stats mentor for Statistically Speaking membership, and a workshop instructor. Read more about Jeff here.

Four Critical Steps in Building Linear Regression Models

While you’re worrying about which predictors to enter, you might be missing issues that have a big impact your analysis. This training will help you achieve more accurate results and a less-frustrating model building experience.

Take Me to The Video!

Tagged as: Linear Regression Model, Regression through the origin, remove intercept