PCA

Four Common Misconceptions in Exploratory Factor Analysis

by Christos Giannoulis, PhD

Today, I would like to briefly describe four misconceptions that I feel are commonly perceived by novice researchers in Exploratory Factor Analysis:

Misconception 1: The choice between component and common factor extraction procedures is not so important.

In Principal Component Analysis, a set of variables is transformed into a smaller set of linear composites known as components. This method of analysis is essentially a method for data reduction.

In Factor Analysis, How Do We Decide Whether to Have Rotated or Unrotated Factors?

by Karen Grace-Martin 1 Comment

I recently gave a free webinar on Principal Component Analysis. We had almost 300 researchers attend and didn’t get through all the questions. This is part of a series of answers to those questions.

If you missed it, you can get the webinar recording here.

Question: How do we decide whether to have rotated or unrotated factors?

Answer:

Great question. Of course, the answer depends on your situation.

When you retain only one factor in a solution, then rotation is irrelevant. In fact, most software won’t even print out rotated coefficients and they’re pretty meaningless in that situation.

But if you retain two or more factors, you need to rotate.

Unrotated factors are pretty difficult to interpret in that situation. [Read more…] about In Factor Analysis, How Do We Decide Whether to Have Rotated or Unrotated Factors?

In Principal Component Analysis, Can Loadings Be Negative?

by Karen Grace-Martin 1 Comment

Here’s a question I get pretty often: In Principal Component Analysis, can loadings be negative and positive?

Answer: Yes.

Recall that in PCA, we are creating one index variable (or a few) from a set of variables. You can think of this index variable as a weighted average of the original variables.

The loadings are the correlations between the variables and the component. We compute the weights in the weighted average from these loadings.

The goal of the PCA is to come up with optimal weights. “Optimal” means we’re capturing as much information in the original variables as possible, based on the correlations among those variables.

So if all the variables in a component are positively correlated with each other, all the loadings will be positive.

But if there are some negative correlations among the variables, some of the loadings will be negative too.

An Example of Negative Loadings in Principal Component Analysis

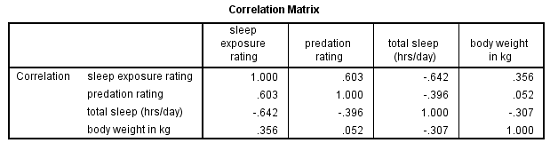
Here’s a simple example that we used in our Principal Component Analysis webinar. We want to combine four variables about mammal species into a single component.

The variables are weight, a predation rating, amount of exposure while sleeping, and the total number of hours an animal sleeps each day.

If you look at the correlation matrix, total hours of sleep correlates negatively with the other 3 variables. Those other three are all positively correlated.

It makes sense — species that sleep more tend to be smaller, less exposed while sleeping, and less prone to predation. Species that are high on these three variables must not be able to afford much sleep.

Think bats vs. zebras.

Likewise, the PCA with one component has positive loadings for three of the variables and a negative loading for hours of sleep.

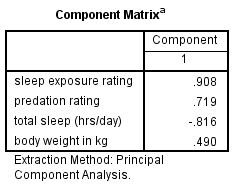
Species with a high component score will be those with high weight, high predation rating, high sleep exposure, and low hours of sleep.

How To Calculate an Index Score from a Factor Analysis

by Karen Grace-Martin 15 Comments

One common reason for running Principal Component Analysis (PCA) or Factor Analysis (FA) is variable reduction.

In other words, you may start with a 10-item scale meant to measure something like Anxiety, which is difficult to accurately measure with a single question.

You could use all 10 items as individual variables in an analysis–perhaps as predictors in a regression model.

But you’d end up with a mess.

Not only would you have trouble interpreting all those coefficients, but you’re likely to have multicollinearity problems.

And most importantly, you’re not interested in the effect of each of those individual 10 items on your [Read more…] about How To Calculate an Index Score from a Factor Analysis