Previous Posts
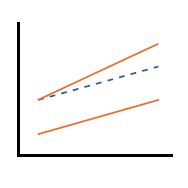
We often have a continuous predictor in a model that we believe has non-constant relationship with the dependent variable along the continuum of the predictor’s range. But how can we be certain? What is the best way to measure this?
Ah, logarithms. They were frustrating enough back in high school. (If you even got that far in high school math.) And they haven’t improved with age, now that you can barely remember what you learned in high school. And yet… they show up so often in data analysis. If you don't quite remember what they are and how they work, they can make the statistical methods that use them seem that much more obtuse. So we're going to take away that fog of confusion about exponents and logs and how they work.
SPSS and Stata use different default categories for the reference category when dummy coding. This directly affects the way to interpret the regression coefficients, especially if there is an interaction in the model.
Structural Equation Modelling (SEM) increasingly is a ‘must’ for researchers in the social sciences and business analytics. However, the issue of how consistent the theoretical model is with the data, known as model fit, is by no means agreed upon: There is an abundance of fit indices available – and wide disparity in agreement on which indices to report and what the cut-offs for various indices actually are.
Have you ever experienced befuddlement when you dust off a data analysis that you ran six months ago? Ever gritted your teeth when your collaborator invalidates all your hard work by telling you that the data set you were working on had "a few minor changes"? Or panicked when someone running a big meta-analysis asks you to share your data? If any of these experiences rings true to you, then you need to adopt the philosophy of reproducible research. Reproducible research refers to methods and tools developed by large software development teams but which can help you keep a sense of order in your data, analysis programs, and results.
Think of reliability as consistency or repeatability in measurements. Not only do you want your measurements to be accurate (i.e., valid), you want to get the same answer every time you use an instrument to measure a variable. That instrument could be a scale, test, diagnostic tool – obviously, reliability applies to a wide range of devices and situations. So, why do we care? Why make such a big deal about reliability?
A few years back the winning t-shirt design in a contest for the American Association of Public Opinion Research read "Weighting is the Hardest Part." And I don't think the t-shirt was referring to anything about patience! Most statistical methods assume that every individual in the sample has the same chance of selection. Complex Sample Surveys are different. They use multistage sampling designs that include stratification and cluster sampling. As a result, the assumption that every selected unit has the same chance of selection is not true. To get statistical estimates that accurately reflect the population, cases in these samples need to be weighted. If not, all statistical estimates and their standard errors will be biased. But selection probabilities are only part of weighting.
There are multiple ways to interface with R. Some common interfaces are the basic R GUI, R Commander (the package “Rcmdr” that you use on top of the basic R GUI), and RStudio. When I first started to learn to use R, I was bound and determined to use the basic R GUI. As someone who was already used to programming in SAS, I wasn’t looking for a point-and-click interface like R Commander. These kinds of interfaces are notoriously limiting when it comes to advanced analyses and software capabilities. (Though if I’m being honest, probably 95% or more of my daily tasks could be handled using R Commander). Without knowing much about it, I also didn’t want to use RStudio. It seemed overly-complicated to download an additional software package for something that already functioned on its own. One day though, when working with someone who wanted to use RStudio, I decided to download it and give it a chance. I never went back to using the basic R GUI.
If you are like I was for a long time, you have avoided learning R. You’ve probably heard that there’s a steep learning curve, and that the available documentation is not necessarily user-friendly. Frankly, both things are true, to some extent. The best and worst thing about R is that it is open-source and there is no single company that is responsible for R or your ability to use it. While there is a developer community that maintains a set of standards and regulated documentation, anyone can add new functionality to R through user-created “packages.” This gives R users a large, flexible range of options (once you know how to install the packages, of course!), which can be a major advantage. On the other hand, these packages are as diverse as the users who create them, and they may emphasize different model features, output displays, and even basic methodological principles. Underlying all of this, though, is what I feel is the truly intimidating part of R:
In this video I will answer a question from a recent webinar Random Intercept and Random Slope Models. We are answering questions here because we had over 500 people live on the webinar so we didn't have time to get through all the questions.

 stat skill-building compass
stat skill-building compass