In this video I will answer a question from a recent webinar Random Intercept and Random Slope Models. We are answering questions here because we had over 500 people live on the webinar so we didn't have time to get through all the questions.

In this video I will answer a question from a recent webinar Random Intercept and Random Slope Models. We are answering questions here because we had over 500 people live on the webinar so we didn't have time to get through all the questions.

In this video I will answer a question from a recent webinar Random Intercept and Random Slope Models. We are answering questions here because we had over 500 people live on the webinar so we didn't have time to get through all the questions.

In this video I will answer a question from a recent webinar Random Intercept and Random Slope Models. We are answering questions here because we had over 500 people live on the webinar so we didn't have time to get through all the questions.

In this video I will answer a question from a recent webinar Random Intercept and Random Slope Models. We are answering questions here because we had over 500 people live on the webinar so we didn't have time to get through all the questions.

If your statistical training was typical, it centered on the normal distribution and models that assume the data are normal. And while the normal distribution is incredibly helpful in many applications, it’s easy to forget that it isn’t so “normal” when dealing with actual data. So… what do you do when the normal distribution just doesn’t work?

Pretty much all of the common statistical models we use, with the exception of OLS Linear Models, use Maximum Likelihood estimation. This includes favorites like: All Generalized Linear Models, including logistic, probit, Poisson, beta, negative binomial regression Linear Mixed Models Generalized Linear Mixed Models Parametric Survival Analysis models, like Weibull models Structural Equation Models That's a lot of models. If you've ever learned any of these, you've heard that some of the statistics that compare model fit in competing models require that models be nested. This is particularly important while you're trying to do model building.

Residuals can be a very broad topic - one that most everyone has heard of, but few people truly understand. It’s time to change that. By definition, a “residual” is “the quantity remaining after other things have been subtracted or allowed for.” In statistics, we use the term in a similar fashion. Residuals come in various forms: Standardized Studentized Pearson Deviance But which ones do we use… and why?

Often a model is not a simple process from a treatment or intervention to the outcome. In essence, the value of X does not always directly predict the value of Y. Mediators can affect the relationship between X and Y. Moderators can affect the scale and magnitude of that relationship. And sometimes the mediators and moderators affect each other.

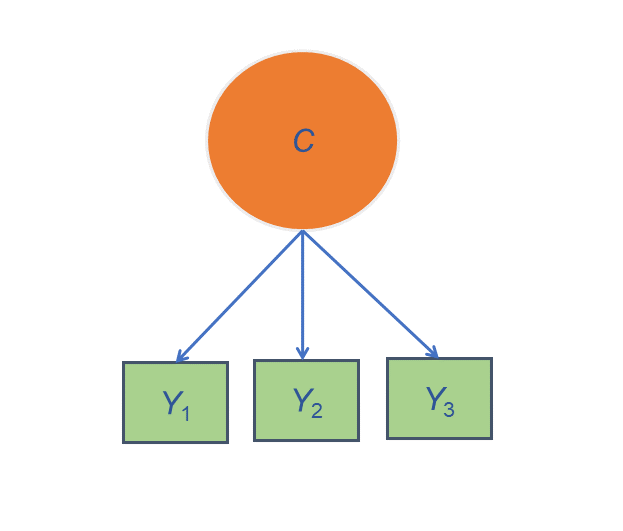
One of the most common—and one of the trickiest—challenges in data analysis is deciding how to include multiple predictors in a model, especially when they’re related to each other. Here's an example. Let's say you are interested in studying the relationship between work spillover into personal time as a predictor of job burnout. You have 5 categorical yes/no variables that indicate whether a particular symptom of work spillover is present (see below). While you could use each individual item, you're not really interested if one in particular is related to the outcome. Perhaps it's not really each symptom that's important, but the idea that spillover is happening. One possibility is to count up the number of items to which each respondent said yes. This variable will measure the degree to which spillover is happening. In many studies, this is just what you need. But it doesn't tell you something important—whether there are certain combinations that generally co-occur, and is it these combinations that affect burnout? In other words, what if it's not just the degree of spillover that's important, but the type? Enter Latent Class Analysis (LCA).