One question that seems to come up pretty often is: What is the difference between logistic and probit regression?   Well, let’s start with how they’re the same: Both are types of generalized linear models. This means they have this form:

We often talk about nested factors in mixed models -- students nested in classes, observations nested within subject. But in all but the simplest designs, it's not that straightforward. In this webinar, you'll learn the difference between crossed and nested factors. We'll walk through a number of examples of different designs from real studies to pull apart which factors are crossed, which are nested, and which are somewhere in between. We'll also talk about a few classic designs, like split plots, Latin squares, and hierarchical data. Particular focus will be on how you can figure all this out in your own design and how it affects how you can and cannot analyze the data.

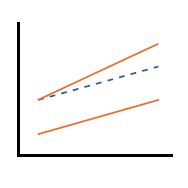
Linear regression with a continuous predictor is set up to measure the constant relationship between that predictor and a continuous outcome. This relationship is measured in the expected change in the outcome for each one-unit change in the predictor. One big assumption in this kind of model, though, is that this rate of change is the same for every value of the predictor. It's an assumption we need to question, though, because it's not a good approach for a lot of relationships. Segmented regression allows you to generate different slopes and/or intercepts for different segments of values of the continuous predictor. This can provide you with a wealth of information that a non-segmented regression cannot.

Here's a common situation. Your grant application or committee requires sample size estimates. It's not the calculations that are hard (though they can be), it's getting the information to fill into the calculations. Every article you read on it says you need to either use pilot data or another similar study as a basis for the values to enter into the software. You have neither. No similar studies have ever used the scale you're using for the dependent variable. And while you'd love to run a pilot study, it's just not possible. There are too many practical constraints -- time, money, distance, ethics. What do you do?

We’ve talked a lot around here about the reasons to use syntax — not only menus — in your statistical analyses. Regardless of which software you use, the syntax file is pretty much always a text file. This is true for R, SPSS, SAS, Stata — just about all of them. This is important because it means you can use an unlikely tool to help you code: Microsoft Word. I know what you're thinking. Word? Really? Yep, it's true. Essentially it's because Word has much better Search-and-Replace options than your stat software’s editor. Here are a couple features of Word’s search-and-replace that I use to help me code faster.

There are many rules of thumb in statistical analysis that make decision making and understanding results much easier. Have you ever stopped to wonder where these rules came from, let alone if there is any scientific basis for them? Is there logic behind these rules, or is it propagation of urban legends? In this webinar, we’ll explore and question the origins, justifications, and some of the most common rules of thumb in statistical analysis.

Think of CFA as a process for testing what you already think you know. CFA is an integral part of structural equation modeling (SEM) and path analysis. The hypothesized factors should always be validated with CFA in a measurement model prior to incorporating them into a path or structural model. Because… garbage in, garbage out. CFA is also a useful tool in checking the reliability of a measurement tool with a new population of subjects, or to further refine an instrument which is already in use.

Question: How do we decide whether to have rotated or unrotated factors? Answer: Great question. Of course, the answer depends on your situation. When you retain only one factor in a solution, then rotation is irrelevant. In fact, most software won't even print out rotated coefficients and they're pretty meaningless in that situation. But if you retain two or more factors, you need to rotate. Unrotated factors are pretty difficult to interpret in that situation.

Question: Can you use Principal Component Analysis with a Training Set Test Set Model? Answer: Yes and no. Principal Component Analysis specifically could be used with a training and test data set, but it doesn't make as much sense as doing so for Factor Analysis. That's because PCA is really just about creating an index variable from a set of correlated predictors.

Question: Can we use PCA for reducing both predictors and response variables? In fact, there were a few related but separate questions about using and interpreting the resulting component scores, so I'll answer them together here.