In a previous article, we discussed how incidence rate ratios calculated in a Poisson regression can be determined from a two-way table of categorical variables.
Statistical software can also calculate the expected (aka predicted) count for each group. Below is the actual and expected count of the number of boys and girls participating and not participating in organized sports.
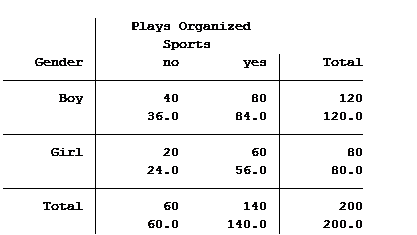
The value in the top of each cell is the actual count (40 boys do not play organized sports) and the bottom value is the expected/predicted count (36 boys are predicted to not play organized sports).
The Poisson model that we ran in the previous article generated the following table:
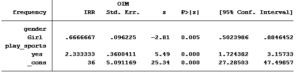
To calculate the predicted values from the Poisson table, we start with the constant (_cons). The constant (aka. intercept) represents the expected value for those in the base category of the categorical variables in the model. In this case the base category for gender is “boys” and for playing sports is “not playing sports”.
Thus the predicted value for boys not playing sports is 36. This is an exact match with the expected number shown in the two way table.
The coefficient for playing sports is 2.333. We interpret this as: for every one person not playing sports, there are 2.33 people who are playing sports.
(If it sounds strange to have 2.33 people playing sports, you can always interpret it as: for every one hundred students not playing sports, there are 233 students who do).
This equates to a predicted value of boys playing organized sports of 2.333 x 36 = 84.
Next, we see from the Poisson model that there are .6667 girls for every boy. The expected number of girls not playing organized sports is .6667 x 36 = 24. The number of predicted girls playing sports is .6667 x 84 = 56.
Both results match the expected values generated in the two-way table.
Note that the total number of boys does not change between the actual and the predicted values. It’s the distribution between playing versus not playing organized sports that changes. The same holds true with the girls. Thus, the incidence rate ratio does not change (80 girls to 120 boys).
These calculations can easily be generated within each statistical software package. For Stata the command is margins gender#play_sports. Confidence intervals can also be calculated for each of the predicted mean frequencies.
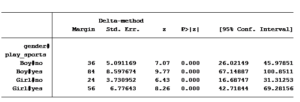
Jeff Meyer is a statistical consultant with The Analysis Factor, a stats mentor for Statistically Speaking membership, and a workshop instructor. Read more about Jeff here.


Hi Jeff,
It was great experience reading your article on STATA.
I would like to ask, what happens when we take log of the independent continuous variable?
How do we interpret their coefficient.