The coefficients of count model regression tables are shown in either logged form or as incidence rate ratios. Trying to explain the coefficients in logged form can be a difficult process.
Incidence rate ratios are much easier to explain. You probably didn’t realize you’ve seen incidence rate ratios before, expressed differently.
Let’s look at an example.
A school district was interested in how many children in their sixth grade classes played on organized sports teams. So they did a count and also noted the gender of the child. The results were put into a table:
| Plays Organized Sports | |||
| Gender | No | Yes | Total |
| Boy | 40 | 80 | 120 |
| Girl | 20 | 60 | 80 |
| Total | 60 | 140 | 200 |
We can see from the table that the ratio of the number of girls to boys in the sixth grade classes is 80 to 120 or 0.667 to 1.
The ratio of the number of those who play sports to the number who do not is 140 to 60 or 2.333 to 1. (We learned about ratios back when we were in sixth grade.)
Girls:Boys = 80/120 = .667
Play Sports:Not Play Sports = 140/60 = 2.333
We don’t usually focus on these ratios in a 2×2 table. Instead, the focus is on the proportions.
Proportion of Girls = 80/200 = .40
Proportion of Boys = 120/200 = .60
What’s interesting, though, is the ratio of girls:boys is the same as the ratio of their proportions:
.40:.60 = .667
The school district superintendent decided to get fancy and create a statistical model. Because we counted the number of boys and girls who played or didn’t play sports, the superintendent suggested we use a count model.
The frequency for each of the four groups (gender by played sports) was the count model’s outcome variable. Our two predictor variables were gender and whether the child played sports.
Not knowing which type of count model to run, the superintendent decided to use a Poisson model. Here are the results:

Here is the statistical software generated two-way table between gender and played sports:
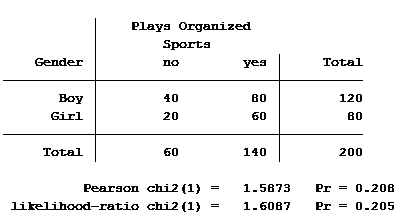
What do you notice from the results?
The incidence rate ratio (IRR) for girl’s is 0.6667. This is the same as the ratio of girls to boys in the table.
The incidence rate ratio for those who played sports to those who did not is 2.3333. This is also the same as the ratio of the number who played sports to the number who did not.
What else do we find?
The Pearson value divided by the degrees of freedom is 1.587, identical to the Pearson chi-square value in the two way table. The deviance value divided by the degrees of freedom is 1.6087, identical to the likelihood-ratio chi-square value shown in the two-way table.
The incidence rate ratio for a binary predictor variable is simply the ratio of the number of events of one category to the number of events in the other category.
For a categorical variable with more than two categories, the IRR is the ratio of the expressed category to the base category.
Jeff Meyer is a statistical consultant with The Analysis Factor, a stats mentor for Statistically Speaking membership, and a workshop instructor. Read more about Jeff here.


In epidemiologic terms an incidence rate is the number/count of new “cases” that occur over a given interval of time, for instance the number of new influenza cases per month during a flu season, whereas prevalance is a snapshot of cases at a single point in time, for instance, the number of influenza cases in NYC on January 1st 2016. I think what you are working with are prevalances/prevalance rates and not incidences/incidence rates.
Hi Dan, I understand your distinction between prevalence and incidence rate in epidemiological terms. In terms of generic count models, we are looking at the difference in incidences over a period of time that is equal for all observations. If it is not equal then we must account for that within the model.
Among the various categories of a categorical variable we are modeling the difference in incidence rate to the base category. This can be looked at as the number of flu cases on a specific date or over a specified period such as “two weeks”. For example, do males have a higher incident rate than females, or infants as compared to teenagers over that period of time.