I recently gave a free webinar on Principal Component Analysis. We had almost 300 researchers attend and didn’t get through all the questions. This is part of a series of answers to those questions.
If you missed it, you can get the webinar recording here.
Question: Can we use PCA for reducing both predictors and response variables?
In fact, there were a few related but separate questions about using and interpreting the resulting component scores, so I’ll answer them together here.
How could you use the component scores?
A lot of times PCAs are used for further analysis — say, regression. How can we interpret the results of regression?
Let’s say I would like to interpret my regression results in terms of original data, but they are hiding under PCAs. What is the best interpretation that we can do in this case?
Answer:
So yes, the point of PCA is to reduce variables — create an index score variable that is an optimally weighted combination of a group of correlated variables.
And yes, you can use this index variable as either a predictor or response variable.
It is often used as a solution for multicollinearity among predictor variables in a regression model. Rather than include multiple correlated predictors, none of which is significant, if you can combine them using PCA, then use that.
It’s also used as a solution to avoid inflated familywise Type I error caused by running the same analysis on multiple correlated outcome variables. Combine the correlated outcomes using PCA, then use that as the single outcome variable. (This is, incidentally, what MANOVA does).
In both cases, you can no longer interpret the individual variables.
You may want to, but you can’t. (more…)
It’s that time of year: flu season.
Let’s imagine you have been asked to determine the factors that will help a hospital determine the length of stay in the intensive care unit (ICU) once a patient is admitted.
The hospital tells you that once the patient is admitted to the ICU, he or she has a day count of one. As soon as they spend 24 hours plus 1 minute, they have stayed an additional day.
Clearly this is count data. There are no fractions, only whole numbers.
To help us explore this analysis, let’s look at real data from the State of Illinois. We know the patients’ ages, gender, race and type of hospital (state vs. private).
A partial frequency distribution looks like this: (more…)
In a previous article, we discussed how incidence rate ratios calculated in a Poisson regression can be determined from a two-way table of categorical variables.
Statistical software can also calculate the expected (aka predicted) count for each group. Below is the actual and expected count of the number of boys and girls participating and not participating in organized sports.
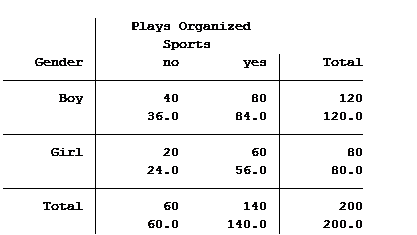
The value in the top of each cell is the actual count (40 boys do not play organized sports) and the bottom value is the expected/predicted count (36 boys are predicted to not play organized sports).
The Poisson model that we ran in the previous article generated the following table: (more…)
The coefficients of count model regression tables are shown in either logged form or as incidence rate ratios. Trying to explain the coefficients in logged form can be a difficult process.
Incidence rate ratios are much easier to explain. You probably didn’t realize you’ve seen incidence rate ratios before, expressed differently.
Let’s look at an example.
A school district was interested in how many children in their sixth grade classes played on organized sports teams. So they did a count and also noted the gender of the child. The results were put into a table: (more…)
The normal distribution is so ubiquitous in statistics that those of us who use a lot of statistics tend to forget it’s not always so common in actual data.
And since the normal distribution is continuous, many people describe all numerical variables as continuous. I get it: I’m guilty of using those terms interchangeably, too, but they’re not exactly the same.
Numerical variables can be either continuous or discrete.
The difference? Continuous variables can take any number within a range. Discrete variables can only take on specific values. For numeric discrete data, these are often, but don’t have to be, whole numbers*.
Count variables, as the name implies, are frequencies of some event or state. Number of arrests, fish (more…)
If you have count data you use a Poisson model for the analysis, right?
The key criterion for using a Poisson model is after accounting for the effect of predictors, the mean must equal the variance. If the mean doesn’t equal the variance then all we have to do is transform the data or tweak the model, correct?
Let’s see how we can do this with some real data. A survey was done in Australia during the peak of the flu season. The outcome variable is the total number of times people asked for medical advice from any source over a two-week period.
We are trying to determine what influences people with flu symptoms to seek medical advice. The mean number of times was 0.516 times and the variance 1.79.
The mean does not equal the variance even after accounting for the model’s predictors.
Here are the results for this model: (more…)