The linear model normality assumption, along with constant variance assumption, is quite robust to departures. That means that even if the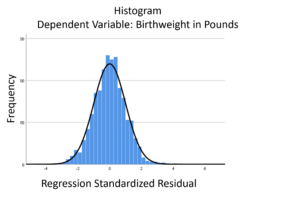 
assumptions aren’t met perfectly, the resulting p-values and confidence intervals will still be reasonable estimates.
This is great because it gives you a bit of leeway to run linear models, which are intuitive and (relatively) straightforward. This is true for both linear regression and ANOVA.
You do need to check the assumptions anyway, though. You can’t just claim robustness and not check. Why? Because some departures are so far off that the p-values and confidence intervals become inaccurate. And in many cases there are remedial measures you can take to turn non-normal residuals into normal ones.
But sometimes you can’t.
Sometimes it’s because the dependent variable just isn’t appropriate for a linear model. The (more…)
What do you do if the assumptions of linear models are violated?
(more…)
Interactions in statistical models are never especially easy to interpret. Throw in non-normal outcome variables and non-linear prediction functions and they become even more difficult to understand. (more…)
When your dependent variable is not continuous, unbounded, and measured on an interval or ratio scale, linear models don’t fit. The data just will not meet the assumptions of linear models. But there’s good news, other models exist for many types of dependent variables.
Today I’m going to go into more detail about 6 common types of dependent variables that are either discrete, bounded, or measured on a nominal or ordinal scale and the tests that work for them instead. Some are all of these.
(more…)
Even if you’ve never heard the term Generalized Linear Model, you may have run one. It’s a term for a family of models that includes logistic and Poisson regression, among others.
It’s a small leap to generalized linear models, if you already understand linear models. Many, many concepts are the same in both types of models.
But one thing that’s perplexing to many is why generalized linear models have no error term, like linear models do. (more…)
What are goodness of fit statistics? Is the definition the same for all types of statistical model? Do we run the same tests for all types of statistic model?
(more…)
assumptions aren’t met perfectly, the resulting p-values and confidence intervals will still be reasonable estimates.