The Analysis Factor
Statistical Consulting, Resources, and Statistics Workshops for Researchers
Based on questions I’ve been asked by clients, most analysts prefer using the factor analysis procedures in their general statistical software to run a confirmatory factor analysis.
While this can work in some situations, you’re losing out on some key information you’d get from a structural equation model. This article highlights one of these.
The last, and sometimes hardest, step for running any statistical model is writing up results.
As with most other steps, this one is a bit more complicated for structural equation models than it is for simpler models like linear regression.
Any good statistical report includes enough information that someone else could replicate your results with your data.
[Read more…] about Member Training: Reporting Structural Equation Modeling Results
by Maike Rahn, PhD
Once you run a factor analysis and think you have some usable results, it’s time to eliminate variables that are not “strong” enough. They are usually the ones with low factor loadings, although additional criteria should be considered before taking out a variable.
As a rule of thumb, your variable should have a rotated factor loading of at least |0.4| (meaning ≥ +.4 or ≤ –.4) onto one of the factors in order to be considered important. [Read more…] about Factor Analysis: A Short Introduction, Part 5–Dropping unimportant variables from your analysis
Factor analysis is a useful tool for investigating variable relationships for complex concepts such as socioeconomic status, dietary patterns, or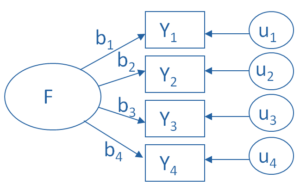 
psychological scales.
It allows researchers to investigate concepts they cannot measure directly. It does this by using a large number of variables to esimate a few interpretable underlying factors.
The key concept of factor analysis is that multiple observed variables have similar patterns of responses because they are all associated with a latent variable (i.e. not directly measured).