Based on questions I’ve been asked by clients, most analysts prefer using the factor analysis procedures in their general statistical software to run a confirmatory factor analysis.
While this can work in some situations, you’re losing out on some key information you’d get from a structural equation model. This article highlights one of these.
The process is very straight forward. Because it’s a confirmatory model, you know the number of factors the variables (indicators) should load onto and specify that number. You make sure each variable has a loading above a specific level and that the indicators that are supposed to load onto the same factor do.
Next you check the Cronbach’s alpha of each construct. The final step is to generate estimated factor scores for each subject in the data set.
Here is an example using data from the International Personality Item Pool, a web based survey tool. The latent construct of interest is the Assertiveness scale. This scale is part of an experimental personality test.
The indicators for this one factor are:
The eigenvalues clearly show a one factor model is appropriate.
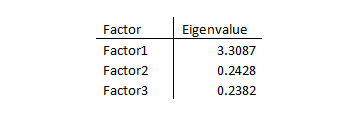
Cronbach’s alpha statistic is excellent as well: .8458.
The factor loadings are all above 0.45. Here is a comparison of the factor loadings using the EFA model and a structural equation model:
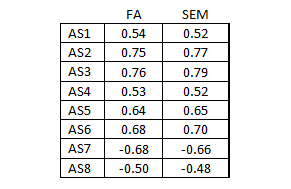
The results are practically identical. So why not use the factor analysis procedure?
Model Fit
Do we have a good model fit?
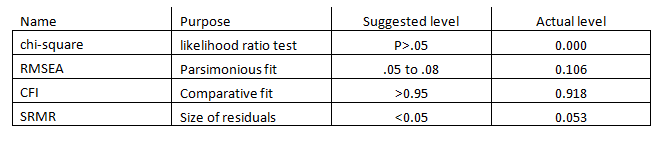
There isn’t a method to determine fit using the factor analysis procedure. Fortunately the structural equation model has several methods. The key model fit statistics for the Assertiveness construct are shown below.
We see that the construct is not within the suggested ranges for a good fitting model.
Understanding Model Fit through Residuals
As with linear regression, SEM lets you examine the standardized residuals to determine goodness of fit. A good fitting model should have the majority of its standardized residuals less than the absolute value of 2.50.
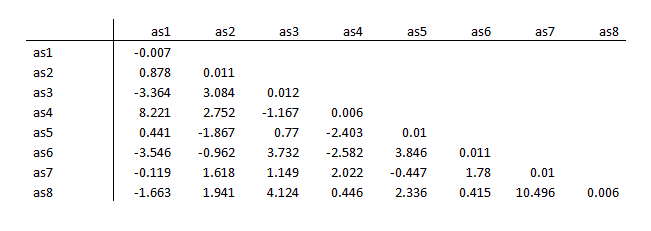
There clearly are some problematic residuals, such as as7/as8 at 10.496.
Understanding Model Fit through Modification Indices
SEM also provides modification indices, which provide information about the specific parts of the model that are leading to poor fits within the model’s variance/covariance structure. Knowing where the model isn’t working can help you decide how to improve the model.
Values greater than 10 are problematic.
Improving the Factor Analysis Model
Using the information provided by the standardized residuals and modification indices, we’re able to refine the measurement of the Assertiveness construct. The new model consists of five indicators, AS3 to AS7. Here are the goodness of fit statistics.
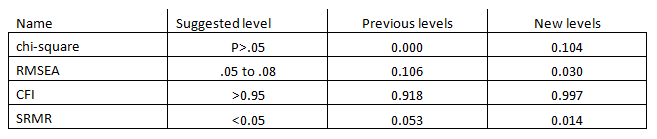
The standardized residuals improved as well.
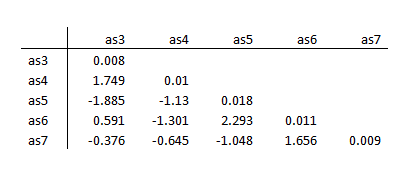
If we use a structural equation model we can be confident we have a well-structured latent construct.
Jeff Meyer is a statistical consultant with The Analysis Factor, a stats mentor for Statistically Speaking membership, and a workshop instructor. Read more about Jeff here.
Very useful materials and interesting topic
What software/package do you use?
Hi,
I am a little confused. You mentioned that doing a CFA using factor analysis method doesn’t give us crucial information. But the example you talked through was an EFA, not a CFA. Don’t most statistical software allow us to do CFA and provide us with the various fit indices, covariance matrix etc (as you described for SEM)?
Hi,
Yes, the initial step I took was an EFA to determine the number of factors. The software I use, Stata, uses the same command for running an EFA and CFA (factor) and I used that as the starting point of the conversation. I’m unaware of any software producing the goodness of fit statistics such as RMSEA, CFI, TLI and SRMR when using the “factor analysis method”. Perhaps there is a package in R? Additionally, the factor analysis method doesn’t produce the variance/covariance standardized residuals which are derived from the difference between the actual data matrix and the model’s estimated matrix.
Thanks for your question,
Jeff
Doesn’t CFA require a fairly large sample?
Hi, the required sample size depends upon how many indicators are in the construct and how high are the loadings. A construct with 3 indicators and loadings around 0.5 would require 150 to 200 observations. A construct with 6 indicators and loadings above 0.75 might only require a sample size of only 40 to 50. These numbers come from running simulations to determine required sample sizes.
Jeff
Probably a good idea to mention that one should not just willy nilly apply the Mod Indices for error covariances to the model without reasonable justification.
You are absolutely correct. I discuss that in detail in the SEM workshop that I teach.
Hi,
If my diagram path is unreliable, how do I correct my model building?
Thank you!
I don’t see how SEM fits into this presentation. It appears that everything that was done was best thought of as a CFA. My understanding of SEM in its simplest sense is that it involves regressing one latent variable onto another. There was no such regression in this presentation, so I don’t know why it was called SEM. It appeared to be simply scale development using CFA.
Hi Michael,
Structural equation modeling consists of two components, a measurement model and a structural model. The CFA is analyzed as a component of the measurement model. Path analysis and regressing one latent variable on another variable is the structural model.
Overall the structural equation model can be described using path diagrams. Each latent construct has paths going to the indicators of the construct. The regression component has arrows going from the predictors to the dependent variable. Within a structural equation model they are all tied in together.
We have a series of articles coming out on SEM. We started with the measurement model because if your constructs are poor fitting your structural model will be unreliable. There is a process to correct model building.
Thanks for your question,
Jeff Meyer