Zero One Inflated Beta Models for Proportion Data

Proportion and percentage data are tricky to analyze.

Much like count data, they look like they should work in a linear model.

They’re numeric. They’re often continuous.

And sometimes they do work. Some proportion data do look normally distributed so estimates and p-values are reasonable.

But more often they don’t. So estimates and p-values are a mess. Luckily, there are other options. One is beta regression.

Beta Regression

Like logistic and Poisson regression, beta regression is a type of generalized linear model.

It works nicely for proportion data because the values of a variable with a beta distribution must be continuous and fall between 0 and 1.

It’s a bit of a funky distribution in that it’s shape can change a lot depending on the values of the mean and dispersion parameters.

Here are a few examples of the possible shapes of a beta distribution, with different means and variances:

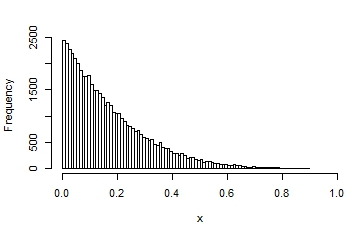
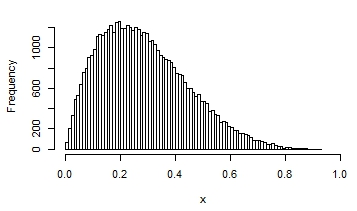
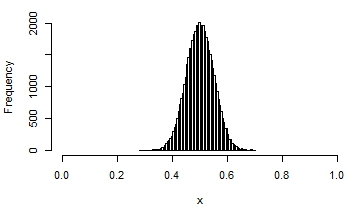
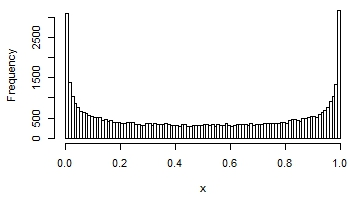
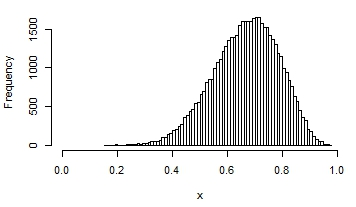
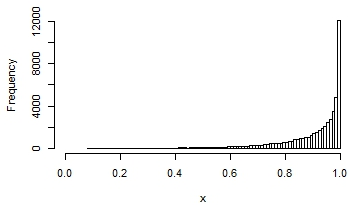
You can see that in some, the distribution looks quite normal. It that situation, you would get reasonable interval estimates and p-values if you assumed normality.

But here is just the kind of sticky situation you commonly see in real data. Let’s say you want to compare the mean proportion of time that people do some behavior–take their prescribed medication, sit, or act physically aggressively toward peers.

Maybe you’ve got some intervention that you want to test will help people take their medications. Perhaps the control group indeed looks like the nice normal distribution in the third graph above.

But the treatment worked so well that in the intervention group, the distribution is highly skewed.  It looks like the last graph.

Assuming normality isn’t going to work here. That’s where a beta regression can work instead.

One big problem.

0 and 1 aren’t possible values in a beta distribution. So if Y|X follows a beta distribution, Y can have values close to 0 and 1, say .001 or .998.  But not 0 or 1 exactly.

So if a client takes their medication 300 out of 300 days, a beta regression won’t run.  You can’t have any 0s or 1s in the data set.

Zero-One Inflated Beta Models

There is, however, a version of beta regression model that can work in this situation. It’s one of those models that has been around in theory for a while, but is only in the past few years become available in (some) mainstream statistical software.

It’s called a Zero-One-Inflated Beta and it works very much like a Zero-Inflated Poisson model.

And it’s a type of mixture model that says there are really three processes going on.

One is a process that distinguishes between zeros and non-zeros. The idea is there is something qualitatively different about people who never take their medication than those who do, at least sometimes.

Likewise, there is a process that distinguishes between ones and non-ones. Again, there is something qualitatively different about people who always take their medication than those who do sometimes or never.

And then there is a third process that determines how much someone takes their medication if they do some of the time.

The first and second processes are run through a logistic regression and the third through a beta regression.

These three models run simultaneously. They can each have their own set of predictors and their own set of coefficients.  For example, maybe memory is a big predictor of how often someone takes their medication if they take it sometimes, but not at all an issue for whether or not someone takes it 0 times. Perhaps those people aren’t forgetting–they can’t afford to purchase it.

So maybe whether someone has health insurance that pays for the medication is a predictor in the zero/non-zero logistic regression, but not in the other two parts.

Depending on the shape of the distribution, you may not need all three processes. If there are no zeros in the data set, you may only need to accommodate inflation at 1.

It’s highly flexible and adds important options to your data analysis toolbox.

Poisson and Negative Binomial Regression for Count Data

Learn when you need to use Poisson or Negative Binomial Regression in your analysis, how to interpret the results, and how they differ from similar models.

Take Me to The Video!