Every once in a while, I work with a client who is stuck between a particular statistical rock and hard place. It happens when they’re trying to run an analysis of covariance (ANCOVA) model because they have a categorical independent variable and a continuous covariate.
The problem arises when a coauthor, committee member, or reviewer insists that ANCOVA is inappropriate in this situation because one of the following ANCOVA assumptions are not met:
1. The independent variable and the covariate are independent of each other.
2. There is no interaction between independent variable and the covariate.
If you look them up in any design of experiments textbook, which is usually where you’ll find information about ANOVA and ANCOVA, you will indeed find these assumptions. So the critic has nice references.
However, this is a case where it’s important to stop and think about whether the assumptions apply to your situation, and how dealing with the assumption will affect the analysis and the conclusions you can draw.
An Example
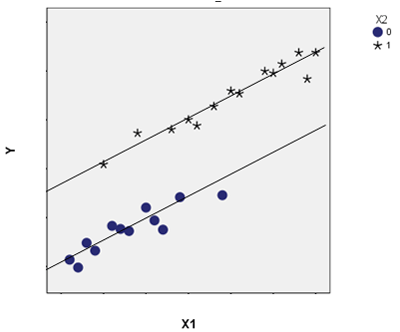
A very simple example of this might be a study that examines the difference in heights of kids who do and do not have a parasite. Since a large contributor to children’s height is age, this is an important control variable.
In this graph, you see the relationship between age X1, on the x-axis and height on the y-axis at two different values of X2, parasite status. X2=0 indicates group of children who have the parasite and X2=1 is the group of children who do not.
Younger children tend to be afflicted with the parasite more often. That is, the mean age (mean of X1) of the blue dots is clearly lower than the mean age of the black stars. In other words, the ages of kids with the parasite are lower than those without.
So the independence between the independent variable (parasite status) and the covariate (age) is clearly violated.
How to Deal with Violation of the ANCOVA Assumptions
These are your options:
1. Drop the covariate from the model so that you’re not violating the assumptions of ANCOVA and run a one-way ANOVA. This seems to be the popular option among most critics.
2. Retain both the covariate and the independent variable in the model anyway.
3. Categorize the covariate into low and high ages, then run a 2×2 ANOVA.
Option #3 is often advocated, but I hope you will soon see why it’s unnecessary, at best. Arbitrarily splitting a numerical variable into categories is just throwing away good information.
Let’s examine option #1.
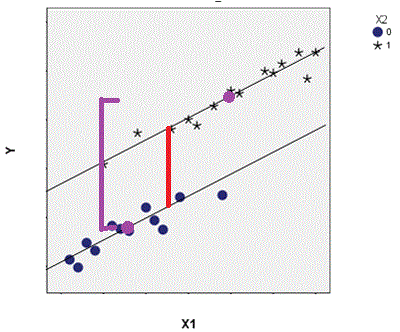
You can see the problem with it in the graph–it doesn’t accurately reflect the data or the relationships among the variables.
With the covariate in the model, the difference in the mean height for kids with and without the parasite is estimated for children at the same age (the height of the red line).
If you drop the covariate, the model estimates the difference in mean height at the overall mean for each group (the purple line).
In other words, any effect of age will be added to the effect of parasite status. And this means you’ll overstate the effect of the parasite on the mean difference in children’s heights.
Why is it an assumption of ANCOVA, then?
You are probably asking yourself “why on earth would this be an assumption of ANCOVA if removing the covariate leads us to overstate relationships?”
To understand why, we need to investigate the problem this assumptions is addressing.
In the analysis of covariance section of Geoffrey Keppel’s excellent book, Design and Analysis: A Researcher’s Handbook, he states:
“It [ANCOVA] is used to accomplish two important adjustments: (1) to refine estimates of experimental error and (2) to adjust treatment effects for any differences between the treatment groups that existed before the experimental treatments were administered. Because subjects were randomly assigned to the treatment conditions [emphasis mine], we would expect to find relatively small differences among the treatments on the covariate and considerably larger differences on the covariate among the subjects within the different treatment conditions. Thus the analysis of covariance is expected to achieve its greatest benefits by reducing the size of the error term [emphasis Keppel’s]; any correction for pre-existing differences produced a random assignment will be small by comparison.”
A few pages later he states,
“The main criterion for a covariate is a substantial linear correlation with the dependent variable, Y. In most cases, the scores on the covariate are obtained before the initiation of the experimental treatment…Occasionally the scores are gathered after the experiment is completed. Such a procedure is defensible only when it is certain that the experimental treatment did not influence the covariate…The analysis of covariance is predicated on the assumption that the covariate is independent of the experimental treatments.”
In other words, it’s about not tainting the inferences you draw by experimentally manipulated treatments. If a covariate was related to the treatment, it would indicate a problem with random assignment. Or it would indicate that the treatments themselves caused the covariate values. These are very important considerations in experiments.
If however, as in our parasite example, the main categorical independent variable is observed and not manipulated, the independence assumption between the covariate and the independent variable is irrelevant.
It’s a design assumption. It’s not a model assumption.
The only effect of the assumption of the independent variable and the covariate being independent is in how you interpret the results.
So what is the appropriate solution?
The appropriate response is #2. Keep the covariate in the analysis. And don’t interpret results from an observational study as if they were from an experiment.
Doing so will lead to a more accurate estimate of the real relationship between the independent variable and the outcome. Just make sure you’re saying that this is the mean difference at any given value of the covariate.
The last issue then becomes: If your critic has banned the word ANCOVA because you don’t have an experiment, what do you call it?
Now it’s down to semantics. It is accurate to call it a general linear model, a multiple regression, or (in my option), an ANCOVA. (I have never seen anyone balk at calling an analysis an ANOVA when the two categorical IVs were related).
The critics who get hung up on this assumption usually want a specific name. General Linear Model is too ambiguous for them. I’ve had clients who had to call it a multiple regression, even though the main independent variable was the categorical one.
One option is use “categorical predictor variable” instead of “independent variable” when describing the variable in the ANCOVA. The latter implies manipulation; the former does not.
This is a case where it’s worth fighting for your analysis, but not the name. The point of all this is communicating results accurately.



Hi Karen,
I am working on my thesis and I have planned on doing a ANCOVA. I have 3 IVs (categorical; 1 and 2) and 3 covariates. It is an experiment meaning the IVs were manipulated and randomized.
The assumption of homogenity of slopes is not met and I am struggling on 1) Do I keep the analyses? and 2) How do I call it? and 3) What and how do I mention the outcomes in my thesis?
Any help would be appreciated.
Greetings,
Isabelle
If it were me, I’d keep the analysis and call it a multiple regression or a general linear model. And then make inferences appropriately. Those assumptions of parallel slopes are about specific inferences. Your data indicate those inferences aren’t going to work, so listen to your data.
That said, you may have to educate your committee on this as they may push back on it. See: https://www.theanalysisfactor.com/when-to-fight-for-your-analysis-and-when-to-jump-through-hoops/
Hi Karen,
I have a three way ANOVA testing the effect of phosphorus (5 rates) x water-logging x cultivar (one water-logging tolerant, one not) on shoot biomass. I’m using R to do the analysis. Half way through the experiment we had to spray the plants with an insecticide due to insect attack. This happened at around the same time as we started the water-logging treatment. After the insecticide spay, plants started showing signs of damage due to the spray (not typical water-logging damage but a burning of the leaves). The damage became progressively worse and was mostly evident in the plants that were waterlogged and in cultivars intolerant to water-logging. Clearly the cultivars less tolerant to water-logging were weakened by the treatment effect of water-logging and were more susceptible to being damaged by the spray. Towards the end of the experiment, I used a score of either 0,1,2,3,4 to measure the damage done by the spray, 0 being no damage 4 being more than 75 % damage. The insect spray had a marked effect on biomass which was evident when graphing the data in R, in addition to the fact a few plants died due to the spray.
How do I include the count data of the spray damage into my analysis? Firstly, the spray damage is correlated with the water-logging treatment and with cultivar (cultivars that were waterlogged and intolerant to water-logging had the most damage, which is the same effect as you you expect to see in the treatment effects on biomass without the spray damage). So dose this violate our ANCOVA assumption of non-correlated variables? Secondly, the spray score is count data, so how does this affect my model?
Also, how do we deal with outliers in R? Im using excel to read in my data to R. Im also measuring the same effects above but intead of biomass i measured isoflavones in leaves. The data errors were not normally distributed and variances were unequal. I used a robust ANOVA to deal with the unequal variances, however, there are a few outliers that need to be removed first, and the robust ANOVA does not work when there are values missing in excel. So what to do about the outliers?
Hi Elliott,
There is a lot there. I would say a few things in response. If you need more help than this, please consider our Statistically Speaking membership.
1. I think those aren’t really counts, they’re ordinal ratings. See Five Ways to Analyze Ordinal Variables (Some Better than Others)
2. It sounds like you should add it as a factor into your model. Include as many interations as you can with the other 3 variables (it’s not clear to me if every plant got sprayed).
Hello Karen.
I am afraid that I cannot agree with your conclusion. Your example leads to an extrapolation of data to ranges that were not captured. The group of children do not cover the same age ranges. No covariates will allow yo to correct for this. For instance, imagine that the influence of parasites on growth changes drastically when they get older (e.g., in pre-pubescence), you would not be able to know. Wouldn’t it be better advise to collect data from children without parasites in the same range like your group with parasites? This is of course a toy example, But in real world complex datasets, ANCOVAs can lead (and have often led) to wildly misleading conclusions.
Hiya,
This section is really helpful. I violate the assumption but am performing an observational study, therefore the assumption is irrelevant as you state. However, are there any references for this?
Thanks,
Leng
Leng,
This is a hard one for a reference. It’s just about a different context.
Hi Karen
This has been very helpful to me. I am using ANCOVA to test the differences in neonatal deaths across regions while controlling for age of the mother, the number of antenatal care visits and the number of tetanus doses. The data is secondary from a cross-sectional population and the assumption of homogeneity of variances is violated. Nearly all the responses provided relate to experimental data, do they apply too cross-sectional secondary data?
Thank you, Imelda
Hi Karen,
Thank you for many useful informations. I would like to cite this article in my final school work, but I cannot find the date of publishing. Do you remember it?
Thanks a lot,
Kate
The question remains–what to do when the covariate is causally influenced by the treatment? You have made a case that sounds like it is still better to retain the covariate (to avoid adding the effect of the covariate, as shown in your figure). Conceptually I don’t fully understand the caution surrounding the assumption–aren’t you still using the covariate to control for a source of variation?
Imagine you are testing the effect on blood pressure of a medication against a control. You know BMI has an effect on blood pressure so want to control for the effect of BMI at the time blood pressure is taken. Let’s say it turns out the medication had an effect on BMI–isn’t it still better to include BMI in the model to test for blood pressure controlling for BMI? What is the alternative?
Yes, absolutely. Keep the covariate in the model.
The problem is that some reviewers will (incorrectly) tell you that you cannot put that covariate in the model b/c ANCOVA assumes no relationship between X and the Covariate.
Good Day,
What happens if all assumptions are violated, except Levene’s AND, you don’t have sufficient participants but cannot continue recruiting?
Hi Dee,
That’s a pretty big question. I’d have to dig into the details with you to decide what to do there. If you want help, I would suggest joining our membership and coming to the next Q&A session. That will allow us to ask you about all the details.
This was excellent, thank you!
how to find out the post test adjusted means of ANCOVA analysis?
If you run the ANCOVA as a multiple regression, you can then take the regression equation and graph it in excel.
Hi,
In my study I´m comparing the Pain Rate Scale between 3 groups of patients who had undergone 3 different types of surgery. These 3 groups have different times of follow-up. So I want to perfom a ANCOVA to analyse if my co-variate (time of follow-up) has influence in my outcome (Pain Rate Scale). However there are significantly differences of followup time between groups. Can I run ANCOVA in this situation?
Thank you for your time
Can I still compute ancova when the covariate violates normality? The IVs were normal with the DV. The DV was significant in the KS normality test at P = .019… My covariate is gender, and closer examination revealed that only males were significant for the ks test.
use of ANCOVA to test the effectiveness of some intervention as a change in a variable (DV) in simple pre post study design with only one group (witot any control group) controlling for the change in some other covariate (s) due to that intervention??? possible?
Any extra assumptions for ANCOVA using two covariates which are linearly correlated to each other, and to the dependent variable, if at all usable??
Hi Karen,
I have a problem with the violation of the independence between the covariate (education) and age groups (6 age groups, 20-29, 30-39, 40-49, 50-59, 60-69, 70-80). Basically the oldest group shows lower education than any other group. According to your tips I can include the covariate in the Mancova anyway (dependent variables are divergent thinking scores), given that the main categorical independent variable (age group) is observed and not manipulated. Am I right? I have noted in many papers, published even in important journals, that on the basis of the lack of indipendence between the covariate and the independent variable authors justify the inclusion of the covariate in the model. They not even mention the violation of the assumption.
Yet, in reporting the results, I also have another huge doubt. I see that the covariate is not significant in the Mancova, but the main independent variable is significant. When running the Ancovas the covariate is significant, as well as the indenpendent variable. Well, should I ignore the significance of the covariate given that it is not significant in the Mancova? I mean, should I apply a concept similar to ANOVA followed by pairwise treatment comparisons or post-hoc comparisons only if the general ANOVA F-test is significant.
Thank you very very very much for any help you can give me!
With best regards,
Max.
Hello
I am having an issue with comparing a pretest-posttest scenario.
I have an initial pretest on 32 students. Half the students received an intervention and the other half did not. I am comparing the post-test scores between the intervention group and the control group.
How do I do this? Apparently I have to account for baseline (pretest) and cannot do a simple t-test comparison between both post-test groups.
Thank you!
Hi, Karen,
Thanks for this information. I am curious, as I am dealing with a violation of homogeneity of regression slopes, what are your thoughts on using the Johnson-Neyman (J-N) technique (Johnson and Neyman, 1936) and Picked-Points Analysis (PPA) as suggested in Huitema, B. (2011). The Analysis of Covariance and Alternatives: Statistical Methods for Experiments, Quasi-Experiments, and Single-Case Studies. Hoboken, NJ: Wiley?
Hi karen,
If the covariate doesn’t correlate the dependent variable using the analysis of correlation in spss, is it nessary to use ANCVOA to adust covariate?
with best regards
shen
Hi Karen,
My IV has three different levels (three conditions). I would like to test if the effects of these three conditions on the DV differentially depend on a questionnaire assessing individual differences (Cov). I find a significant interaction between IV x Cov. Now, I would like to follow-up on this by comparing the slopes for the three conditions in order to make interpretations. I wonder how to do this in SPSS? Thank you so much in advance.
With kind regards,
Desiree
Hi Karen
Is there a way to read old newsletters please? You said above in one for your replies (@Feyza) that there was a newsletter on ANCOVA and I would love to read it but I’m not sure where could I find it.
Thanks
Hi Susel,
We put all the newsletter articles onto the blog, although there is usually a few weeks delay, as we want our subscribers to get first dibs.
If you just type ANCOVA in the search box on the right, you’ll get all our articles on ANCOVA.
Hi Karen,
Thank you so much for explaining so well all about ANCOVA!
I have similar problem regarding my independent variable and one of the covariates. I am conducting experiment and i have two treatments – one with the manipulated effect and one control. Since i am working with texts as stimuli i have also tested whether they are equally perceived as credible and believable. Unfortunately, in the manipulated group, the text is perceived to be more credible. Thus my question, how can i extract the influence of text credibility from my manipulation?
Thank you so much!
Hi Paka,
Exactly as specified in the article. Include credibility as a covariate, then compare the groups at one value of credibility. Explain all of this in your write up, and don’t overstate your conclusions.
Hi Karen,
I have exactly the same problem. I used ANCOVA and homogeneity of slopes assumption is unvalid at my study. So, can’t I use ANCOVA? If I can use, isn’t it important that the assumption is not valid? How can I explain this situation in my thesis?
Your answer is so important for me. Thanks.
Feyza
Hi Feyza,
Your question inspired my September 2013 newsletter. 🙂 It’s going out today, so you may want to subscribe if you haven’t already. 🙂
Karen
I think Categarizing the numerical variable in subgroups will not affect the the result for one reson, the group of the sample were colected randomly, together with the fact that the choise was determened (let say detemined by the age and the hieght of the sample (the kids). furthermore, you can design the assumtion so as to decrease the overestimatiom or lets go further, even to avoid it. in my limited thinking, there is pros and cons of comparing the results or out puts of the observation with the experment, in the sense that the former I assume you my be participant obserfer with-out influencing your subjects and you may be biased or not considering the imput of your supjects. In the experiment you still have that bais again, in the sense that the results depends in the interperetation. Thank you for the brain storming, I hope that make some sense, I’m interested in your feedback.
Hi
I hope someone can help me with this. I am quite inexperienced with stats so any advice is most welcomed (and hopefully I will understand it! 🙂
I am doing research on organisational change and looking at how certain types of change (e.g. closures of offices, layoffs, investment on activities/functions) have affected seven psychological variables (commitment, trust in leaders, procedural fairness, perception of organisational support, etc.).
Now, I want to know how the changes (related to the types of organisational change described above) in the content of the psychological contract (measured through four of the psychological variables) impact organisational commitment (if at all). My original idea was to run an analysis of covariance in SPSS, but in checking for the basic assumptions I found that the regression slopes are not homogeneous, and that is the end of ANCOVA according to several authors.
I am left without a clear idea of how to circumvent this problem. What kind of analysis can be performed when a) the covariates and the factor (type of change) are related and b) when the regression slopes are not homogeneous?
Please, bear in mind that mine is NOT an experimental design, rather observational, change happens without my intervention and I just look at an internal survey that studies the psychological and demographic variables.
Many thanks in advance.
Hi Susel,
Just run a linear model. Call it a regression if you like, gut I would run it in the General Linear Model in SPSS. Include an interaction term between the covariate and the factor.
Hi Karen,
Thanks for explaining things so clearly on your website. I have exactly the same problem and question as ‘Stats’ posted on October 28th at 7:35am. Particularly, because in your example you didn’t cover what to do when the homogeneity of slopes assumption is violated. If you could still provide an answer to ‘stats’ I think that would help a lot of people.
thanks so much
Thanks, stats2. I must have missed that one.
And it’s not necessarily a problem, as I mentioned above.
And fyi, we go over this in detail, with examples, in one of my workshops, Interpreting (Even Tricky) Regression Coefficients. You may want to check it out. http://theanalysisinstitute.com/ebook-interpreting-linear-regression/
Quick question: how you would interpret ANCOVA results if p-value is less than 0.05 and R-squared is 0.001?
Thanks.
You’d conclude that this very small effect would be seen in any sample and can be trusted.
Karen
ANCOVA is somewhat ANOVA of regression residuals. R-squared value say there is no fit with data, meaning residuals are useless and, you say that even if R-squared value is so tiny, I can make my inference based solely on p-value? Please, correct me if I’m wrong. Thank you!
Hi Karen,
Thanks for the tips. I had the same problem in my analysis…What I had been worrying about is overestimating the effect of fixed factor, which positively interacts with the covariate. What can I do to limit the overestimation, if I simply wanna know the effect of the fixed factor?
Thank you!
Helena
Hi Helena,
You’re welcome. You just have to be clear in your writeup that the effect of the fixed factor differs depending on the value of the covariate. Giving a few different examples of the size of the fixed effect at high and low covariate values can help.
Karen
Hi Karen,
Thanks for this. I’m just wondering about the assumption of homogeneity of regression with an ANCOVA. I have some situations where all other assumptions are met, however the covariate and independent variable interact. I have looked at this is two ways (I am using SPSS). Firstly by doing a custom model with IV*CV and checking that the significance is >0.05. Secondly by constructing a CV vs DV scatterplot then drawing different regression lines for each IV and comparing these.
My questions are:
Do I need to check this assumption if my study is randomised and the CV is measured before the IV is given (the CV in this case is the ‘pre’ intervention measure, the DV is the ‘post’ measure, and the IV is an intervention)?
How different are the slopes allowed to be? Is there a difference in r2 that is considered acceptable?
What do I do if the interaction is significant? some places talk about doing a Johnson-Neyman test instead but that doesn’t look easy to do on SPSS. And they also mention a Wilcox procedure, but I’m not sure is that the same as a Wilcoxon rank test?
Thanks in advance!
Hi Stats,
Once again, I would say that if there is an interaction between the IV and the CV, then you can’t ignore it. Yes, it means that the slopes of the relationship between the CV and the DV are different for your intervention and control group.
This isn’t always bad. Say the intervention basically equalized people–regardless of their pretest score, they all did very well on the postest. No relationship between pretest and posttest.
But in the control group, there is a strong relationship between pre and post.
I would say that this is one possible good outcome and an interesting one. The parallel slopes assumption says that the intervention affected all people equally. So people low on the pretest stayed the lowest, but were bumped up just as much as people who started off at the top. Depending on what you’re studying, that may not be good.
Just run the GLM, say there is an interaction, and explain the interaction effect. You may have to call it a multiple regression or a GLM instead of ANCOVA, but it may be the most interesting effect!
Once again, your teaching skills are remarkable. In one post, I understand many things that I was previously taught, but not in an intuitive way.
Thank you so much, and please… don’t stop !