There are two types of bounded data that have direct implications for how to work with them in analysis: censored and truncated data. Understanding the difference is a critical first step when undertaking a statistical analysis.

Principal Component Analysis is really, really useful. You use it to create a single index variable from a set of correlated variables. In fact, the very first step in Principal Component Analysis is to create a correlation matrix (a.k.a., a table of bivariate correlations). The rest of the analysis is based on this correlation matrix. You don't usually see this step -- it happens behind the scenes in your software. Most PCA procedures calculate that first step using only one type of correlations: Pearson. And that can be a problem. Pearson correlations assume all variables are normally distributed. That means they have to be truly quantitative, symmetric, and bell shaped. And unfortunately, many of the variables that we need PCA for aren't. Likert Scale items are a big one.

Outliers are one of those realities of data analysis that no one can avoid. Those pesky extreme values cause biased parameter estimates, non-normality in otherwise beautifully normal variables, and inflated variances. Everyone agrees that outliers cause trouble with parametric analyses. But not everyone agrees that they’re always a problem, or what to do about them even if they are. Sometimes a nonparametric or robust alternative is available--and sometimes not. There are a number of approaches in statistical analysis for dealing with outliers and the problems they create.

The LASSO model (Least Absolute Shrinkage and Selection Operator) is a recent development that allows you to find a good fitting model in the regression context. It avoids many of the problems of overfitting that plague other model-building approaches. In this month's Statistically Speaking webinar, guest instructor Steve Simon, PhD, will explain what overfitting is -- and why it's a problem.

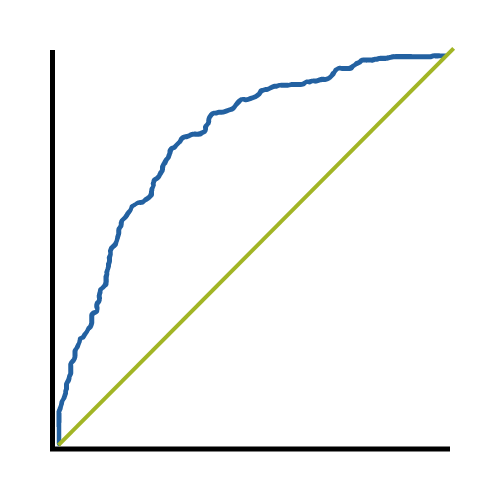
An incredibly useful tool in evaluating and comparing predictive models is the ROC curve. Its name is indeed strange. ROC stands for receiver operating characteristic. Its origin is from sonar back in the 1940s; ROCs were used to measure how well a sonar signal (e.g., from a submarine) could be detected from noise (a school of fish). In its current usage, ROC curves are a nice way to see how any predictive model can distinguish between the true positives and negatives. In order to do this, a model needs to not only correctly predict a positive as a positive, but also a negative as a negative. The ROC curve does this by plotting sensitivity, the probability of predicting a real positive will be a positive, against 1-specificity, the probability of predicting a real negative will be a positive. (A previous newsletter article covered the specifics of sensitivity and specificity, in case you need a review about what they mean--and why it's important to know how accurately the model is predicting positives and negatives separately.) The best decision rule is high on sensitivity and low on 1-specificity. It's a rule that predicts most true positives will be a positive and few true negatives will be a positive. I've been talking about decision rules, but what about models?

In this webinar, we’ll provide a gentle introduction to generalized linear mixed models (or GLMMs). You’ll become familiar with the major issues involved in working with GLMMs so you can more easily transition to using these models in your work.

In a previous post we discussed the difficulties of spotting meaningful information when we work with a large panel data set. Observing the data collapsed into groups, such as quartiles or deciles, is one approach to tackling this challenging task. We showed how this can be easily done in Stata using just 10 lines of code..

Panel data provides us with observations over several time periods per subject. In this first of two blog posts, I’ll walk you through the process. (Stick with me here. In Part 2, I’ll show you the graph, I promise.)

The concept of a statistical interaction is one of those things that seems very abstract. If you’re like me, you’re wondering: What in the world is meant by “the relationship among three or more variables”?

When you have data measuring the time to an event, you can examine the relationship between various predictor variables and the time to the event using a Cox proportional hazards model. In this webinar, you will see what a hazard function is and describe the interpretations of increasing, decreasing, and constant hazard. Then you will examine the log rank test, a simple test closely tied to the Kaplan-Meier curve, and the Cox proportional hazards model.