Confusing Statistical Term #10: Mixed and Multilevel Models

What’s the difference between Mixed and Multilevel Models? What about Hierarchical Models or Random Effects models?

I get this question a lot.

The answer: very little.

There are small differences, but they’re more about style than substance. In other words, you’re never choosing among them as the appropriate analysis. Whichever one you call your analysis, you’re going to run them the same way.

The terminology problem in statistics

It’s astounding to me the number of names that textbook authors, software companies, and statistical professors come up with for the same basic thing.

This happens in other parts of statistics as well, so this isn’t in any way unique to these models.

I’m not positive, but I think it happens when people working in a specific area of research, with specific data needs, find the general term confusing. They’d prefer a more intuitive term that makes sense to people in their field. So they invent a new one for a particular type of model, as it applies to a particular type of design or data.

But over the years, I’ve found it causes more confusion than clarity. And statistics is confusing enough.

What defines these models

All of the models I’m talking about here have two types of effects: fixed and random. The fixed effects are just like the effects in any regression model. They measure the effect of fixed predictors. They’re in the equation below in blue.

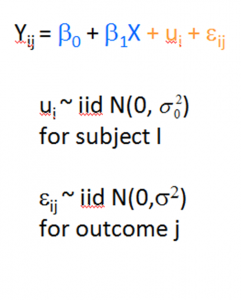The random effects are important in these models because they account for the non-independence of the response variable that occurs due to some sort of clustering of observations. They’re in the equation in orange.

An example is a data set in which students are clustered within schools. Students from the same school are likely to have more similar responses than students from different schools.

A model that investigates the relationship between predictors about the students and/or schools and some outcome measured for each student needs to account for this effect of school. When this effect of school is only there to account for the non-independence, it’s a random effect.

So all these models include both fixed effects of predictors and random effects introduced by the design.

The many names of these models

Below I’ve listed a few names I’ve seen for these models. There are others. Sometimes there is no distinction among them. Their name differences only come from emphasizing specific parts of the models. And sometimes the different names imply a specific design structure of the data, which affects specific terms included in the model.

Multilevel Models (MLM)
Hierarchical Linear Models (HLM)

Both are pretty generic names, but they imply the random factors are nested/hierarchical, not crossed. They often use separate model equations for each level. They use slightly different notation and terminology than mixed models. Their focus is on levels, not random factors. Their notation and terminology doesn’t really accommodate crossed random factors.

Mixed Effects Models (LME)
Mixed Models
Random Effects Models

These are the most generic names for these models. They often use a single model equation, and the notation and terminology are a little more flexible than in multilevel model. Including “Linear” in the name specifies that these apply to continuous outcomes and assume normal residuals. These are in contrast to Generalized Linear versions of these models.

Random Coefficient Models
Random Intercept and Slope Models

Intercepts and slopes are types of coefficients, or effects. So using these names makes it clear exactly which random effects are being used. I’ve seen Random Coefficient specifically imply a random slope, but not always.

Crossed Random Effects Models

These are commonly seen in experimental data, but not exclusively. They imply a specific design where two or more random factors are crossed, not nested.

Individual Growth Curve Models

These are specifically random slope models, where the “cluster” variable is an individual and the slope is over time. They have their own name because they’re used so commonly in longitudinal data.

How to analyze mixed and multilevel models

Regardless of what you call them, the analysis doesn’t change. You’re going to use either software designed specifically for these models, like HLM or MLWin, or a procedure in general statistical software that can accommodate both fixed and random effects. There are often multiple options in each software, but I’ve listed common ones here:

•    SAS: Proc Mixed
•    Stata: mixed or any command starting with xt or me
•    SPSS: mixed
•    R: lmer

Random Intercept and Random Slope Models

Get started with the two building blocks of mixed models and see how understanding them makes these tough models much clearer.

Take Me to The Video!