If you have run mixed models much at all, you have undoubtedly been haunted by some version of this very obtuse warning: “The 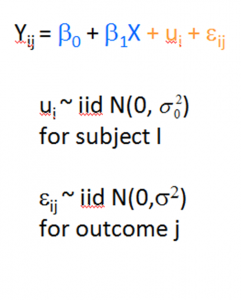 Hessian (or G or D) Matrix is not positive definite. Convergence has stopped.”
Hessian (or G or D) Matrix is not positive definite. Convergence has stopped.”
Or “The Model has not Converged. Parameter Estimates from the last iteration are displayed.”
What on earth does that mean?
Let’s start with some background. If you’ve never taken matrix algebra, (more…)
One of those tricky, but necessary, concepts in statistics is the difference between crossed and nested factors.
As a reminder, a factor is any categorical independent variable. In experiments, or any randomized designs, these factors are often manipulated. Experimental manipulations (like Treatment vs. Control) are factors.
Observational categorical predictors, such as gender, time point, poverty status, etc., are also factors. Whether the factor is observational or manipulated won’t affect the analysis, but it will affect the conclusions you draw from the results.
(more…)
Are you learning Multilevel Models? Do you feel ready? Or in over your head?
It’s a very common analysis to need to use. I have to say, learning it is not so easy on your own. The concepts of random effects are hard to wrap your head around and there is a ton of new vocabulary and notation. Sadly, this vocabulary and notation is not consistent across articles, books, and software, so you end up having to do a lot of translating.
(more…)
When you hear about multilevel models or mixed models, you very often think of a nested design. Level 1 units  nested in Level 2 units, which are in turn possibly nested in Level 3 units. But these variables that define the units and that become random factors in the model can, in fact, be crossed with each other, not nested.
nested in Level 2 units, which are in turn possibly nested in Level 3 units. But these variables that define the units and that become random factors in the model can, in fact, be crossed with each other, not nested.
(more…)
What is the difference between Clustered, Longitudinal, and Repeated Measures Data? You can use mixed models to analyze all of them. But the issues involved and some of the specifications you choose will differ.
Just recently, I came across a nice discussion about these differences in West, Welch, and Galecki’s (2007) excellent book, Linear Mixed Models.
It’s a common question. There is a lot of overlap in both the study design and in how you analyze the data from these designs.
West et al give a very nice summary of the three types. Here’s a paraphrasing of the differences as they explain them:
- In clustered data, the dependent variable is measured once for each subject, but the subjects themselves are somehow grouped (student grouped into classes, for example). There is no ordering to the subjects within the group, so their responses should be equally correlated.
- In repeated measures data, the dependent variable is measured more than once for each subject. Usually, there is some independent variable (often called a within-subject factor) that changes with each measurement.
- In longitudinal data, the dependent variable is measured at several time points for each subject, often over a relatively long period of time.
A Few Observations
West and colleagues also make the following good observations:
1. Dropout is usually not a problem in repeated measures studies, in which all data collection occurs in one sitting. It is a huge issue in longitudinal studies, which usually require multiple contacts with participants for data collection.
2. Longitudinal data can also be clustered. If you follow those students for two years, you have both clustered and longitudinal data. You have to deal with both.
3. It can be hard to distinguish between repeated measures and longitudinal data if the repeated measures occur over time. [My two cents: A pre/post/followup design is a classic example].
4. From an analysis point of view, it doesn’t really matter which one you have. All three are types of hierarchical, nested, or multilevel data. You would analyze them all with some sort of mixed or multilevel analysis. You may of course have extra issues (like dropout) to deal with in some of these.
My Own Observations
I agree with their observations, and I’d like to add a few from my own experience.
1. Repeated measures don’t have to be repeated over time. They can be repeated over space (the right knee gets the control operation and the left knee gets the experimental operation). They can also be repeated over condition (each subject gets both the high and low cognitive load condition. Longitudinal studies are pretty much always over time.
This becomes an issue mainly when you are choosing a covariance structure for the within-subject residuals (as determined by the Repeated statement in SAS’s Proc Mixed or SPSS Mixed). An auto-regressive structure is often needed when some repeated measurements are closer to each other than others (over either time or space). This is not an issue with purely clustered data, since there is no order to the observations within a cluster.
2. Time itself is often an important independent variable in longitudinal studies, but in repeated measures studies, it is usually confounded with some independent variable.
When you’re deciding on an analysis, it’s important to think about the role of time. Time is not important in an experiment, where each measurement is a different condition (with order often randomized). But it’s very important in a study designed to measure changes in a dependent variable over the course of 3 decades.
3. Time may be measured with some proxy like Age or Order. But it’s still really about time.
4. A longitudinal study does not have to be over years. You could be measuring reaction time every second for a minute. In cases like this, dropout isn’t an issue, although time is an important predictor.
5. Consider whether it makes sense to think about time as continuous or categorical. If you have only two time points, even if you have numerical measurements for them, there is no point in treating it as continuous. You need at least three time points to fit a line, but more is always better.
6. Longitudinal data can be analyzed with many statistical methods, including structural equation modeling and survival analysis. You only use multilevel modeling if the dependent variable is measured repeatedly and if the point of the model is to see how it changes (or differs).
Naming a data structure, design, or analysis is most helpful if it is so specific that it defines yours exactly. Your repeated measures analysis may not be like the repeated measures example you’re trying to follow. Rather than trying to name the analysis or the data structure, think about the issues involved in your design, your hypotheses, and your data. Work with them accordingly.
Go to the next article or see the full series on Easy-to-Confuse Statistical Concepts
One of the difficult decisions in mixed modeling is deciding which factors are fixed and which are random. And as difficult as it is, it’s also very important. Correctly specifying the fixed and random factors of the model is vital to obtain accurate analyses.
Now, you may be thinking of the fixed and random effects in the model, rather than the factors themselves, as fixed or random. If so, remember that each term in the model (factor, covariate, interaction or other multiplicative term) has an effect. We’ll come back to how the model measures the effects for fixed and random factors.
Sadly, the definitions in many texts don’t help much with decisions to specify factors as fixed or random. Textbook examples are often artificial and hard to apply to the real, messy data you’re working with.
Here’s the real kicker. The same factor can often be fixed or random, depending on the researcher’s objective. (more…)
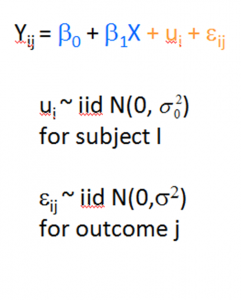 Hessian (or G or D) Matrix is not positive definite. Convergence has stopped.”
Hessian (or G or D) Matrix is not positive definite. Convergence has stopped.”

