Based on questions I’ve been asked by clients, most analysts prefer using the factor analysis procedures in their general statistical software to run a confirmatory factor analysis.
While this can work in some situations, you’re losing out on some key information you’d get from a structural equation model. This article highlights one of these.
by Christos Giannoulis
Many data sets contain well over a thousand variables. Such complexity, the speed of contemporary desktop computers, and the ease of use of statistical analysis packages can encourage ill-directed analysis.
It is easy to generate a vast array of poor ‘results’ by throwing everything into your software and waiting to see what turns up. (more…)
After you are done with the odyssey of exploratory factor analysis (aka a reliable and valid instrument)…you may find yourself at the beginning of a journey rather than the ending.
The process of performing exploratory factor analysis usually seeks to answer whether a given set of items form a coherent factor (or often several factors). If you decide on the number and type of factors, the next step is to evaluate how well those factors are measured.
There are two main types of factor analysis: exploratory and confirmatory. Exploratory factor analysis (EFA) is data driven, such that the collected data determines the resulting factors. 
Confirmatory factor analysis (CFA) is used to test factors that have been developed a priori.
Think of CFA as a process for testing what you already think you know.
CFA is an integral part of structural equation modeling (SEM) and path analysis. The hypothesized factors should always be validated with CFA in a measurement model prior to incorporating them into a path or structural model. Because… garbage in, garbage out.
CFA is also a useful tool in checking the reliability of a measurement tool with a new population of subjects, or to further refine an instrument which is already in use.
Elaine will provide an overview of CFA. She will also (more…)
One of the many confusing issues in statistics is the confusion between Principal Component Analysis (PCA) and Factor Analysis (FA).
They are very similar in many ways, so it’s not hard to see why they’re so often confused. They appear to be different varieties of the same analysis rather than two different methods. Yet there is a fundamental difference between them that has huge effects on how to use them.
(Like donkeys and zebras. They seem to differ only by color until you try to ride one).
Both are data reduction techniques—they allow you to capture the variance in variables in a smaller set.
Both are usually run in stat software using the same procedure, and the output looks pretty much the same.
The steps you take to run them are the same—extraction, interpretation, rotation, choosing the number of factors or components.
Despite all these similarities, there is a fundamental difference between them: PCA is a linear combination of variables; Factor Analysis is a measurement model of a latent variable.
PCA’s approach to data reduction is to create one or more index variables from a larger set of measured variables. It does this using a linear combination (basically a weighted average) of a set of variables. The created index variables are called components.
The whole point of the PCA is to figure out how to do this in an optimal way: the optimal number of components, the optimal choice of measured variables for each component, and the optimal weights.
The picture below shows what a PCA is doing to combine 4 measured (Y) variables into a single component, C. You can see from the direction of the arrows that the Y variables contribute to the component variable. The weights allow this combination to emphasize some Y variables more than others.
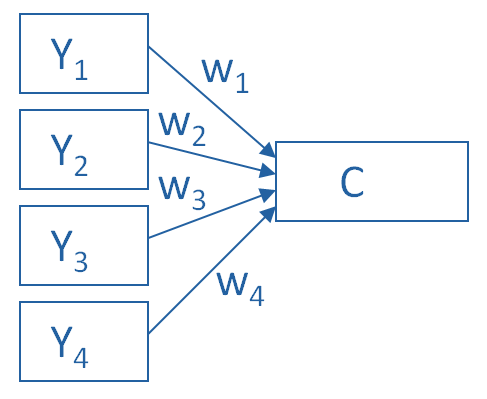
This model can be set up as a simple equation:
C = w1(Y1) + w2(Y2) + w3(Y3) + w4(Y4)
A Factor Analysis approaches data reduction in a fundamentally different way. It is a model of the measurement of a latent variable. This latent variable cannot be directly measured with a single variable (think: intelligence, social anxiety, soil health). Instead, it is seen through the relationships it causes in a set of Y variables.
For example, we may not be able to directly measure social anxiety. But we can measure whether social anxiety is high or low with a set of variables like “I am uncomfortable in large groups” and “I get nervous talking with strangers.” People with high social anxiety will give similar high responses to these variables because of their high social anxiety. Likewise, people with low social anxiety will give similar low responses to these variables because of their low social anxiety.
The measurement model for a simple, one-factor model looks like the diagram below. It’s counter intuitive, but F, the latent Factor, is causing the responses on the four measured Y variables. So the arrows go in the opposite direction from PCA. Just like in PCA, the relationships between F and each Y are weighted, and the factor analysis is figuring out the optimal weights.
In this model we have is a set of error terms. These are designated by the u’s. This is the variance in each Y that is unexplained by the factor.
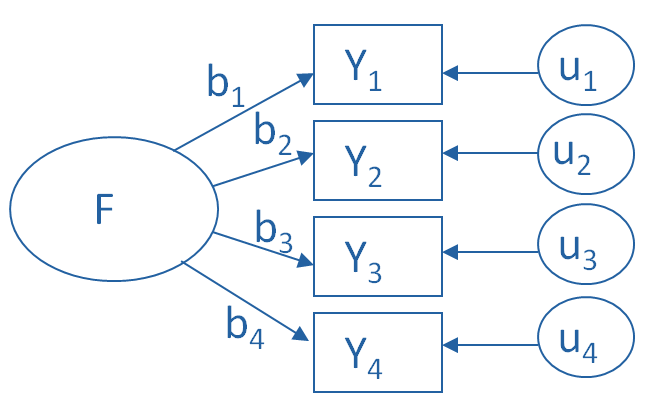
You can literally interpret this model as a set of regression equations:
Y1 = b1*F + u1
Y2 = b2*F + u2
Y3 = b3*F + u3
Y4 = b4*F + u4
As you can probably guess, this fundamental difference has many, many implications. These are important to understand if you’re ever deciding which approach to use in a specific situation.
By Manolo Romero Escobar
What is a latent variable?
“The many, as we say, are seen but not known, and the ideas are known but not seen” (Plato, The Republic)
My favourite image to explain the relationship between latent and observed variables comes from the “Myth of the Cave” from Plato’s The Republic. In this myth a group of people are constrained to face a wall. The only things they see are shadows of objects that pass in front of a fire (more…)