by Jeff Meyer
It’s that time of year: flu season.
Let’s imagine you have been asked to determine the factors that will help a hospital determine the length of stay in the intensive care unit (ICU) once a patient is admitted.
The hospital tells you that once the patient is admitted to the ICU, he or she has a day count of one. As soon as they spend 24 hours plus 1 minute, they have stayed an additional day.
Clearly this is count data. There are no fractions, only whole numbers.
To help us explore this analysis, let’s look at real data from the State of Illinois. We know the patients’ ages, gender, race and type of hospital (state vs. private).
A partial frequency distribution looks like this:
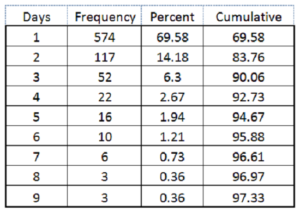
90% of those admitted to the ICU are discharged within 3 days.
But there are patients that stay quite a few days. What are the characteristics of those patients that stay longer?
To find out, we run a linear regression using the predictors mentioned above and get the following results:
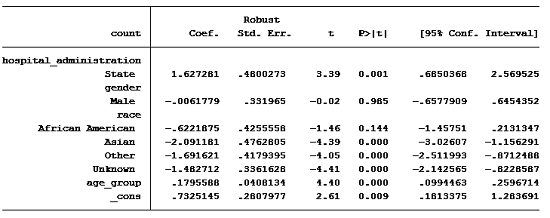
We see that we have a number of significant predictors.
We tell the hospital we can figure out how long a patient might stay in the ICU, and we create a histogram of the expected length of stay:
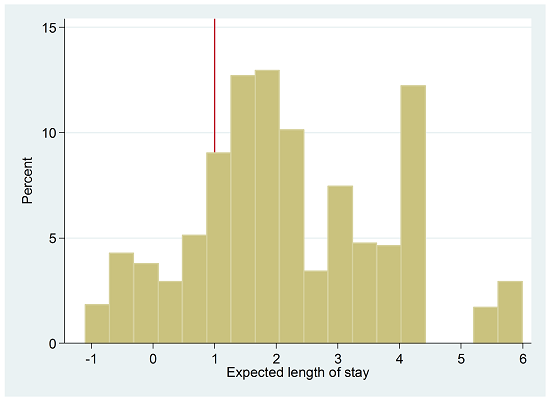
We notice there are quite a few patients that stay less than 1 day: 167 out of 818 observations (20%). But we know that can’t be right.
What went wrong?
You can’t use a linear regression on truncated data. If you do, you will get bad results.
We’ll discuss truncated count models in module 4 of our upcoming workshop, Analyzing Count Data: Poisson, Negative Bimonial, and Other Essential Models.
Jeff Meyer is a statistical consultant with The Analysis Factor, a stats mentor for Statistically Speaking membership, and a workshop instructor. Read more about Jeff here.
Leave a Reply