The concept of a statistical interaction is one of those things that seems very abstract. Obtuse definitions, like this one from Wikipedia, don’t help:
In statistics, an interaction may arise when considering the relationship among three or more variables, and describes a situation in which the simultaneous influence of two variables on a third is not additive. Most commonly, interactions are considered in the context of regression analyses.
First, we know this is true because we read it on the internet! Second, are you more confused now about interactions than you were before you read that definition?
If you’re like me, you’re wondering: What in the world is meant by “the relationship among three or more variables”? (As it turns out, the author of this definition is referring to an interaction between two predictor variables and their influence on the outcome variable.)
But, Wikipedia aside, statistical interaction isn’t so bad once you really get it. (Stay with me here.)
Let’s take a look at the interaction between two dummy coded categorical predictor variables.
The data set for our example is the 2014 General Social Survey conducted by the independent research organization NORC at the University of Chicago. The outcome variable for our linear regression will be “job prestige.” Job prestige is an index, ranked from 0 to 100, of 700 jobs put together by a group of sociologists. The higher the score, the more prestigious the job.
We’ll regress job prestige on marital status (no/yes) and gender.
First question: Do married people have more prestigious jobs than non-married people?
The answer is yes. On average, married people have a job prestige score of 5.9 points higher than those not married.
Next question: Do men have jobs with higher prestige scores than women?
The answer is no. Our output tells us there is no difference between men and women as far as the prestige of their job. Men’s average job prestige score is only .18 points higher than women, and this difference is not statistically significant.
But can we conclude that for all situations? Is it possible that the difference between job prestige scores for unmarried men and women is different than the difference between married men and women? Or will it be pretty much the same as the table above?
Here’s where the concept of interaction comes in. We need to use an interaction term to determine that. With the interaction we’ll generate predicted job prestige values for the following four groups: male-unmarried, female-unmarried, male-married and female-married.
Here are our results when we regression job prestige on marital status and gender and the interaction between married and male:
Everything is significant, but how in the world do we read this table? We are shown 4 values: married = 4.28, male = -1.86, married & male = 3.6 and the constant is 41.7. It helps to piece together the coefficients to create the predicted scores for the four groups mentioned above.
Let’s start with the constant. It’s in every regression table (unless we make the decision to exclude it). What exactly does it represent? The constant represents the predicted value when all variables are at their base case. In this situation our base case is married equals no and gender equals female (married = 0 and gender = 0).
So an unmarried woman has on average a predicted job prestige score of 41.7. An unmarried man’s score is calculated by adding the coefficient for “male” to the constant (unmarried woman’s score plus the value for being a male): 41.7-1.9 = 39.8.
To calculate a married woman’s score we start with the constant (unmarried female) and add to it the value for being married: 41.7 + 4.3 = 46
How do we calculate a married man’s score? Always start with the constant and then add to it any of the factors that belong to it. So we’ll need to add to the constant the value of being married, of being male and also the extra value for being married and male: 41.7 + 4.3 – 1.9 + 3.6 = 47.7.
Notice that the difference in average job prestige score between unmarried women and unmarried men is 1.9 greater and the difference in average job prestige score between married women and married men is 1.7 less. The difference in those differences is 3.6 (1.9 – (-1.7), which is exactly the same as the coefficient of our interaction.
For those of you who use Stata, the simple way to calculate the predicted values for all four groups is to use the post-estimation command margins.
margins sex#married, cformat(%6.2f)
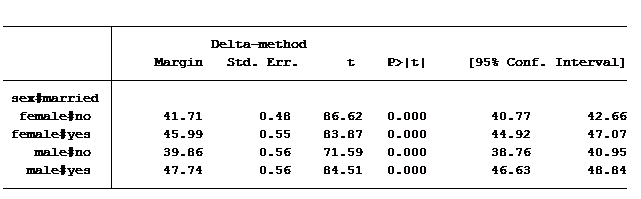
(These same means can be calculated using the lsmeans option in SAS’s proc glm or using EMMeans in SPSS’s Univariate GLM command).
If we had not used the interaction we would have concluded that there is no difference in the average job prestige score between men and women. By using the interaction, we found that there is a different relationship between gender and job prestige for unmarried compared to married people.
So that’s it. Not so bad, right? Now go forth and analyze.
Jeff Meyer is a statistical consultant with The Analysis Factor, a stats mentor for Statistically Speaking membership, and a workshop instructor. Read more about Jeff here.

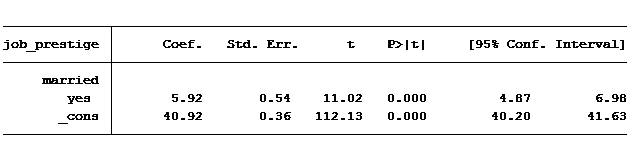
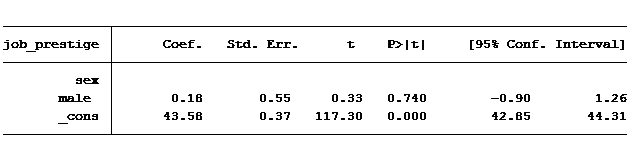
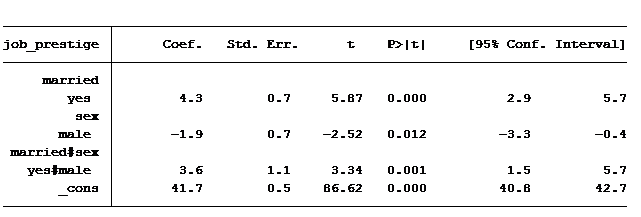

This is so helpful thanks so muhc
Yours is one of the best explanations for interpreting and modeling the interaction of dummy variables. I particularly like your simplistic way of identifying the categories associated with the dummy variables.
Do you have advice on how to interpret interactions between two categorical variables in logit model regressions (not linear)?
Hi Amirah,
Those are harder because instead of the interaction being a difference in mean differences, it’s a ratio of odds ratios. I’m not sure I could explain it well in something as short as a blog post but I’ll give it a try soon.
In a linear regression model, the β coefficient for an interaction term estimates a deviation from the sum of treatment subgroup effects (or differences in mean differences); whereas, in the case of non-linear regression models like Logistic regression and other exponential models, the β coefficient for an interaction term estimates a deviation from the product of treatment subgroup
effects. In addition, the former applies a linear scaling while the latter applies a multiplicative scaling. I hope this isn’t too complex an explanation.
Commenting on 2/22/2022 cause it’s cool.
Love the page.
The explanation is great! I finally understood it!
I have one further question:
In my analysis, I have a two-category IV and a three-category moderator. The output table shows only significance for the constant and for one of the interaction terms (out of 6 interaction terms incl. 4 bases).
Can I somehow still interpret the coefficients of the ‘margins command’ or is that only possible for the one interaction that was significant?
Hi, I am very new to this,
How do I create the interaction between my dummy variable and another IV, prior to using that in the regression?
Is there code to conduct the predicted mean estimate in R?
Thank you!
Hi Jeff,
how would you interpret the difference between the main effects (e.g. of being married) in the two models (1. model – without interaction effect, 2.model with interaction). The coefficient is 5.92 in the 1. model but only 4.3 in the 2. model.
Thanks for your support!!
Hi, in the first model without the interaction people who are married have a job prestige score that is 5.92 points higher than non-married people. In the second model married females have a prestige score 4.3 points higher than a non-married female. In the second model we are examining the simple effect, not the main effect.
Hi Jeff,
Assume we didn’t have the first model. Is there a way to calculate the value of 5.92 only by looking at the results of the second model?
Hi Jeff
Very nice explanations in your site. Like it. Why I am finding little different outputs, doing the same way as yours?
. reg prestg10 married sex married#sex
note: 1.married#1b.sex omitted because of collinearity
note: 1.married#2.sex omitted because of collinearity
Source | SS df MS Number of obs = 2,427
————-+———————————- F(3, 2423) = 43.60
Model | 22677.5245 3 7559.17485 Prob > F = 0.0000
Residual | 420115.275 2,423 173.386411 R-squared = 0.0512
————-+———————————- Adj R-squared = 0.0500
Total | 442792.799 2,426 182.519703 Root MSE = 13.168
——————————————————————————
prestg10 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
————-+—————————————————————-
married | 7.785306 .7930514 9.82 0.000 6.230177 9.340436
sex | -1.697658 .7876104 -2.16 0.031 -3.242117 -.1531983
|
married#sex |
0#female | 3.508429 1.077844 3.26 0.001 1.394837 5.622021
1#male | 0 (omitted)
1#female | 0 (omitted)
|
_cons | 41.6048 .9643385 43.14 0.000 39.71379 43.49581
——————————————————————————
Hi,
We have difference because we are working with slightly different data. I didn’t show all of the output. You have 2,427 observations and I’m using 2,425 observations.
Thanks for your question,
Jeff
Hi thanks for the explanation it was a great help. Just want to ask if there is a risk of high multicollinearity among the independent variables given the new interaction dummies included. If there is no such risk, could you kindly explain? Thanks
Hi Tim,
It is very unlikely that you will have increased risk of high multicollinearity when using interactions, especially categorical interactions. With categorical predictors we are concerned that the two predictors mimic each other (similar percentage of 0’s for both dummy variables as well as similar percentage of 1’s). With a 2 by 2 interaction we are actually creating one variable with 4 possible outcomes. If our two categorical predictors are gender and marital status our interaction is now a categorical variable with 4 categories: male-married, male-unmarried, female-married and female-unmarried. There is no multicollinearity issue with our interaction.
Very useful – however, in looking into interactions with dummy-coded variables I have only ever found explanations for between-participants categorical factors. In the ANOVA approach there are different models for repeated measures and no-repeated measures factors. How would one go about using an interaction effect in regression involving a within-participants categorical factor and a continuous variable?
Thank you for this article! What if you are interested in additive-scale interaction between two non-dichotomous variables (i.e., two categorical variables with 4-5 categories each)?
Hi Ariel,
I have never tried running a 4 x 4 interaction. It is possible to run but very difficult to explain the results. My suggestion is to limit one variable to 2 categories and the second variable can have 2 or more categories (2×3, 2×4 etc). This interaction would be explained similarly to a 2×2 interaction.
Jeff
Dear Jeff,
Is it necessary to create centered-mean variables for the dummy variables when you are creating interactions between two dummy variables?
Kind regards,
Michiel
Hi Michiel,
If you are creating a dummy predictor by continuous predictor interaction it is a good idea to center the continuous variable if “0” is not within the range of the observed values for the continuous predictor. However, if you rely upon the results from the emmeans or margins command output to explain your results then centering is not important. If you have a dummy predictor by dummy predictor interaction you would not be centering either dummy predictor because they are not continuous (quantitative) predictors but are categorical (qualitative) predictors.
Jeff
What happens if the interaction term is not significant? Does that mean that the differences between any of the groups are not significant or that differences are not significant only for that group defined by the code of the interaction term?
Hi Elizabeth,
In this example with binary predictors, if the interaction is insignificant for one combination it is insignificant for the other combination. One combination, is the difference between married and unmarried different for males as compared to females. The second combination, is the difference between males and females different for married as compared to unmarried. If you have more than two categories, such as married, unmarried and separated, it is possible that one of the combinations is significant and the others are not. Example, separated vs unmarried for males as compared to females is significant but separated vs married for males as compared to females is not.
Thanks for this wonderful explanation!
One question: What if, say, the coefficient for being married is insignificant, can we still sum up the values to get the predicted value of being male and married? Thank you!
Hi,
I’m glad you found this post helpful. Yes, you follow the same procedure whether married is significant or not.
Hi, can you tell me why contrast and pwcompare give different results?thanks!!!
Sorry, I meant pwcompare and margins..
Hi,
If you use the following command: margins married#sex, the margins command will give you the marginal means for each of the four paired groups.
If you use this command: “margins married#sex,pwcompare”, you will get the differences (contrast) between the different paired groups, the standard errors and the 95% CI for their differences.
This command, “pwcompare married#sex,pveffects”, you will get the differences (contrast) between the different paired groups, the standard errors, t scores and the p values.
Choosing which command to use is a matter of determining what results you are looking to report.
Thanks!!also for replying so quickly!!
Hello,
If I have two dummy independent variables (both binary, with two levels each) in a regression, then how do I construct the the interaction variable? By coding both variables as (1,0) and multiplying them? Let’s say, I put the two dummy coded IVs and their interaction term in a regression, would the p value associated with the resulting main effects and interaction be the same as the p value obtained for the main effects and interaction in an ANOVA? I know that an ANOVA is supposed to be equivalent to a regression, but in an ANOVA, the main effects will be the same regardless of whether I calculate an interaction. Whereas in the regression, if the interaction term is correlated with the two dummy variables, it can affect the estimate (and resulting p values) of the main effect of the two dummy variables (and the interaction term also). Also, in case of interactions, should the dummy variables always be coded as (1,0) or can they also be coded as (1,-1) and then multiplied if I predict a certain type of interaction? Thanks!
In your model code you need to add the interaction. This is not done by multiplying them. If you are using SPSS you would have the following code. Note that the interaction is added in the /DESIGN code and the output to understand the interaction is in the /EMMEANS code. The dummy variables for UNIANOVA are coded 0 and 1.
UNIANOVA job_prestige BY married sex
/EMMEANS=TABLES(married) COMPARE ADJ(BONFERRONI)
/DESIGN=married sex married*sex.
Jeff
In your model code you need to add the interaction. This is not done by multiplying them. If you are using SPSS you would have the following code. Note that the interaction is added in the /DESIGN code and the output to understand the interaction is in the /EMMEANS code. The dummy variables for UNIANOVA are coded 0 and 1.
UNIANOVA job_prestige BY married sex
/EMMEANS=TABLES(married) COMPARE ADJ(BONFERRONI)
/DESIGN=married sex married*sex
Hi, thx for this powerful explanation. I’ve one additional question: how do I interpretate main and interaction effects when I have more than two (interacting) covariates? Which is the base (reference) value and what does the constant mean?
Hi, the base value is the category of the categorical variable that is not shown in the regression table output. The constant is the culmination of all base categories for the categorical variables in your model. For example, let’s say you have 3 predictors, gender, marital status and education in your model. The categories not shown in your output for gender is male, for marital status is single and for education is college graduate, then your constant represents single males with a college degree.
If you have a three way interaction I would suggest you use your software marginal means calculations (margins command in Stata, lmeans in R and SPSS) to help you interpret the results and graph them. In the course I teach on linear models I show how to do this in a spreadsheet as well as using your statistical software to understand the output.
To test the significance of each grouping in a three way interaction you will want to use your software’s pairwise comparison command.
Great!thank you!!!
Hi,
Thanks for your explanation. This help me a lot to understand that i need. However, i used a survey design and possion regression model to estimate prevalence ratio (irr), how is the sintaxis? Currently, My sintaxis is svy linearized: poisson Depresion_1 i.SEXO2 i.ns10_recod i.accidente i.familia i.estres_financiero EDAD, irr
But the reviewer said me that i need to evaluated interaction between sex and the other variables. How can i do this???
Cheers!
The easiest way to create an interaction of one variable with all variables is:
poisson Depresion_1 i.SEXO2##(i.ns10_recod i.accidente i.familia i.estres_financiero c.EDAD), irr
You need to put a “c.” in front of continuous variables such as age (EDAD). The other way to code it is:
poisson Depresion_1 i.SEXO2 i.ns10_recod i.accidente i.familia i.estres_financiero c.EDAD i.SEXO2#i.ns10_recod i.SEXO2#i.accidente i.SEXO2#i.familia i.SEXO2#i.estres_financiero i.SEXO2#c.EDAD, irr
Doing it this way allows you to easily drop any interactions that are not significant.
Jeff
Thanks You very much! it worked!! The analysis showed that there no effect interaction between sex and all other variables (according to p. value).
I’m really sorry I have not been able to answer the comment before and thank you. My computer had “died” and I could not recover the data to do the analysis until now.
But, what numbers means below the variable? is it the the value of each variable that are being test?
SEXO2#ns10_recod
2 2
2 3
Cheers
Hi Gabriel,
Assuming this come from the margins command, the first number 2 of the first line represents the 2nd category of the predictor SEX02 and the second 2 is the second category the the variable ns10_recod. The second line is similar, the 2nd category of SEX02 and the 3rd category of ns10_recod.
Awesome explanation. I just have one question. How do we understand if the difference between the unmarried women and married men is significant? Does it have anything to do with the interaction?
Thanks. Yes, you can test to see if there is a significant difference between unmarried women and married men. You can test any pairing within an interaction. How you do it depends upon your software. In Stata you would use the post estimation command “pwcompare” or “contrast”. In R you can use the “contrast” command and in SPSS you would run your comparisons through the “emmeans” statement within “unianova”.
How would be the interpretation if you’d have a glm with negative binomial distribution?
A negative binomial glm uses an incidence rate ratio (irr) to compare the exponentiated coefficients. A categorical interaction represents how much greater (or less) it is than the base category. For example an IRR of 1.25 can be interpreted as “25% greater than the base category”. If you determine your IRR’s in the similar manner to what is shown in this article you must add the non-exponentiated coefficients and then exponentiate the sums to obtain the IRR’s. It’s much easier if you use your statistical software’s post hoc commands to calculate these such as Stata’s margins command or SPSS EMMeans
Simplified and educative indeed