You In a recent post, I discussed the differences between repeated measures and longitudinal data, and some of the issues that come up in each one. I want to expand on that discussion, and discuss the three approaches you can take to analyze repeated measures data: repeated measures ANOVA, Mixed Models, and Marginal Models.
For a few, very specific designs, you can get the exact same results from all three approaches. This, I find, has always made it difficult to figure out what each one is doing, and how to apply them to OTHER designs.
For the purposes of discussion here, I’m going to define repeated measures data as repeated measurements of the same outcome variable on the same individual. The individual is often a person, but could just as easily be a plant, animal, colony, company, etc. For simplicity, I’ll use “individual.”
Beyond that, anything goes. Measurements can repeat over time or space; time can itself be an important factor in the experiment or not; each individual can have 2 or 20 measurements.
Approach 1: Repeated Measures ANOVA
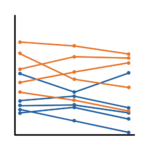When most researchers think of repeated measures, they think ANOVA. In my personal experience, repeated measures designs are usually taught in ANOVA classes, and this is how it is taught.
You set up the data with one row per individual, so individual is the focus of the unit of analysis. This is the wide format.
The multiple measures of the outcome variable are in multiple columns of data. That means we consider each a different variable. It’s a multivariate approach and is run as a MANOVA, so the model equation had multiple dependent variables and multiple residuals. (SPSS users-this is the approach taken by the Repeated Measures (RM) GLM procedure).
The biggest advantage of this approach is its conceptual simplicity. It makes sense. But it has a lot of assumptions that can be very difficult to meet in all but very limited experimental situations.
These include balanced data (if even one observation is missing, the subject will get dropped) and equal correlations among response variables. It also has the limitation that it cannot do post-hoc tests on the repeated measures factor, which I consider a huge limitation.
It tends to work well in many experimental situations, where each measurement is taken under a different experimental condition.
Approach 2: The Marginal Model
The second approach treats the repeated responses as multilevel data. The outcome is a single variable, and another variable indicates the condition or time measurement. This requires that each subject have multiple rows of data in the spreadsheet. You call this the long format, or stacked data. It changes the unit of analysis from the subject to each measurement occasion.
In a marginal model (AKA, the population averaged model), the model equation is written just like any linear model. There is a single response and a single residual. The difference, though, is that in the marginal model we do not assume residuals are independent with constant variance.
In a marginal model, we can directly estimate the correlations among each individual’s residuals. (We do assume the residuals across different individuals are independent of each other). We can specify that they are equally correlated, as in the RM ANOVA, but we’re not limited to that assumption.
Each correlation can be unique, or measurements closer in time can have higher correlations than those farther away. There are a number of common patterns that the residuals tend to take.
Likewise, the residual variances don’t have to be equal as they do in the RM ANOVA.
So in cases where the assumptions of equal variances and equal correlations are not met, we can get much better fitting models by using a marginal model. The other big advantage is by taking a univariate approach, we can do post-hoc tests on the repeated measures factor.
Approach 3: The Linear Mixed Model
Like the marginal model, the linear mixed model requires the data in the long format.
It too controls for non-independence among the repeated observations for each individual, but it does so in a conceptually different way. Rather than estimate the correlation among an individual’s repeated observations, it actually adds one or more random effects for Individuals to the model.
The model equation therefore includes extra parameters for any random effects. They take the form of additional residual terms, and the model estimates the variance of each.
This literally means the model controls for the effects of individual. The simplest mixed model, the random intercept model, controls for the fact that some individuals always have higher values than others. By controlling for this variation, we’ve taken it out of the original residual.
Individual growth curve models are a specific type of mixed model that uniquely models each individual’s value of the outcome over time. They are particularly useful when the research question is about how covariates affect not only the value of the dependent variable, but its change over time.
The biggest advantage of mixed models is their incredible flexibility. They handle clustered individuals as well as repeated measures (even in the same model). They handle crossed random factors as well as nested.
You can treat Time as continuous or categorical. You can measure covariates just once per individual or repeatedly at each observation. Unbalanced data are no problem, and even if some outcomes are missing for some individuals, they won’t be dropped from the model.
The biggest disadvantage of mixed models, at least for someone new to them, is their incredible flexibility. It’s easy to mis-specify a mixed model, and this is a place where a little knowledge is definitely dangerous.
Hi Karen
Thank you for such a useful blog. I got so many of my questions answered from the responses you have given. I managed to run Linear mixed model for my data and got the output but Just can’t interpret the meaning. My data involves 4 days of food diary (macronutrients) in day shift workers and night shift workers. so I have two groups with unequal number of participants and 4 days of repeated measure on diet entries(Calories, proteins, fats and carbs). I am interested in finding the trends in macronutrient intake over 4 days in both the groups and also identify differences in macronutrient intake on all four days.
Also how do we right the results on the basis of mixed model output, What do we report, which tables do we include when writing in a manuscript or even the results section of thesis.
Hi Manjeet,
Here’s some info on how to write it up: https://www.theanalysisfactor.com/writing-results-mixed-models/
Interpretation is harder to answer without fully understanding your design and research questions.
Hi Karen,
great article and linked video!
The data I have suggest to me that a linear mixed model would be most appropriate, but it would be great to get your take on it.
The outcome I have increases linearly and looks normally distributed at baseline and follow-up measurements. We want to see if the rate of increase in the outcome variable differs between groups defined by categories of two binary variables (we want to know if either of the binary variables has an effect and whether there is an interaction).
Number of measurements of the outcome varies between subject as does the time between the measurements.
We want to control for a few covariates (we’re only interested in the effects of abovementioned two binary variables) and those covariates are both categorical and continuous (for example age and gender).
Do you think a linear mixed model might be work or might something like Marginal Multilevel Model be more appropriate?
This is helpful. But I think your Approach 1 is conflating two distinct conceptualizations: Repeated measures versus multivariate. I a repeated measures ANOVA, while “the multiple measures of the outcome variable are in multiple columns of data,” each is considered a *level* (of one or more variables), not “a different variable.”
Hi Richard,
You may think of those as different categories of the same variable, but that’s not what is happening mathematically. When you run a proc glm in SAS with the repeated statement or a Repeated Measures ANOVA in SPSS’s glm, it is literally treating those as different variables. All the multivariate output that you get is MANOVA output.
And slightly off topic, and I know I’m alone on this, but I try not to use “level” to designate “values of a facter/categorical variable” because people mix it up with levels in a multilevel model. Two different meanings of the same word within the same context. Very confusing. But I am reading your comment as meaning the former.
You say that the multivariate approach to repeated measures has the limitation that it cannot do post-hoc tests on the repeated measures factor. Why can’t you use Hotelling’s t-test to do pairwise comparisons or a STP procedure to compare more than two categories? That is what I was taught.
Hi Larry,
Then you’re not accounting for inflated type I error from multiple testing.
Can’t you adjust the alpha as in the Bonferroni or the Roy-Bose procedure?
Yes, you could. But you’re limited to only that very conservative test.
Hi there,
I have hit a problem. I have conducted two tests and I want to do a RMANOVA.
Problem is : the first test contained ten questions, the second test contained 11 questions.
So if a student got 10 points on the first test and 11 on the second he scored the same grade but SPSS doesn’t recognize that.
Is there any way in which I can account for that difference and still run a RMANOVA test that actually says something valid?
Kind regards,
Pim
Hi Pim,
I created that same problem for myself in my senior thesis when I was an undergrad.
This is actually a tricky situation because you have proportions, which aren’t appropriate for ANOVA anyway. I would have to ask you a few questions to really give good advice.
Hi there,
I have a problem on SPSS and really need some help, if possible.
I was originally trying to perform a repeated measures ANCOVA to investigate the effects of time (3 time points) on an continuous outcome variable. I have no missing cases. However, I need to include a time-varying covariate (also a continuous variable). From following some stats books, it appears that a linear mixed model will allow this. I have set the data up in long form, as suggested, and attempted to run the analysis (Analyze-Mixed Model-Linear). I have entered a categorical variable of SUBJECT (coded 1-73 for the number of subjects I have) into the subjects box, and the categorical variable of TIME (coded 1-3) into the repeated box.
On the next box, I have placed my measured dependent variable into the corresponding box, my covariate (time varying continuous measurement) in the covariate box and I’ve placed my TIME factor into the Factors box.
After this, I’m unsure what steps to take in terms of specifying random or fixed effects etc. I basically just need to know if there is a time effect when the covariate is included or not and how to interpret the SPSS output.
Any help would be much appreciated!
Thanks Karen
Hi
What do you mean by model and parameter matrices for repeated measures data in case of multivariate analysis??
Hi Karen,
Thank you for this article! I have a question, if that’s alright –
I am trying to do a mixed design ANOVA (2 levels for the between-subj factor and 4 levels for the within-subj factor), and all I have are the means, standard deviations, and sample sizes. Since I can’t use the regular “click/drop-down menu” method, I am writing syntax for this analysis.
I found how to do a one-way ANOVA (http://www-01.ibm.com/support/docview.wss?uid=swg21476127) and how to do a simple 2×2 or factorial ANOVA (http://www-01.ibm.com/support/docview.wss?uid=swg21475358) using syntax. I’ve been trying to play with this to make a syntax for a mixed design ANOVA, but I am not succeeding; I only keep coming up with a 2×4 factorial ANOVA, which isn’t right based on my data – I definitely need a mixed design ANOVA model.
Any suggestions are much appreciated!! Thank you!
Hi,
I have a question about my thesis.
I have a repeated measures design: snacking measured over 5 weeks.
I have 2 threatment groups (condition)
and i have a extra independent variable: habit tendency (continue)
I would like to know the effect of habit tendency on the outcome in interaction with the two threatment groups.
I think I need to do a multiple regression, but its not possible to use repeated measures in there.
If i do a GLM, i can put the habit tendency as a extra between factor, but i am wondering if thats right to do beceause the variable is continue.
Can you give me some advise?
Thanks, Dorianne
Hi Karen.
It’s lovely to see someone being so helpful.. I am hoping you may be able to offer some advice regarding my undergrad research project as I am completely baffled!
The study design is an RCT and I am interested in determining the difference between two groups of equal size in regards to wound healing rate (defined as % surface area reduction per week). I will be taking measurements at baseline and then weekly for 4 weeks. Would a mixed model be most appropriate or perhaps linear regression?
Many thanks
i m doing thesis for my MD .. i have two group .. i am assesing pain between the group at 5 time point ..how to use repeated measure analysis .????
I think you should use linear mixed model (LMM). Since you have pain scores on the same participants at 5 different points, your data will violate the ” independent observation” assumption for using repeated measures ANOVA or linear regression. Also the LMM will be the only method of analysis if your groups have unequal number of participants or their is any missing data
Hi there,
I am just wondering if I could get some help… I am running a 1 x 3 ANOVA with repeated measures but some of my subjects have missing data and so as you stated are getting “dropped” when I run the test. I am just wondering what test you think I should do instead and if there is a page that shows how to set up the data accordingly.
Thank you,
Britt
Hi Karen
I am just wondering if you could please guide me about GLMM that I have applied on my data, whether its an appropriate method or should I use other methods such as a paired-t-test. I have repeated measures of a species abundance at 32 sites at pre- and post disease stages. I just want to compare abundance differences, so I decided to use GLMM with sites being a random effect since the same sites were surveyed. The dataset format is as below:
Abundance Site Period
587 1 Pre
962 2 Pre
805 3 Pre
1510 4 Pre
.
.
.
361 1 Post
292 2 Post
99 3 Post
485 4 Post
425 5 Post
513 6 Post
.
.
.
#and here is r codes (lme4 package) that I used:
glmm|z|)
(Intercept) 6.063271 0.143635 42.21 <2e-16 ***
PeriodPre 0.865099 0.008847 97.79 <2e-16 ***
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Correlation of Fixed Effects:
(Intr)
PeriodPre -0.043
# Do you think this is a good method or better to use something like a paired test? and how should I represent the results GLMM as a table in my paper, should be like this:
Parameter estimate std. erro z value p-value
Intercept 6.06 0.143 42.2 <0.001
Period (Pre-disease) 0.86 0.008 97.7 <0.001
Thanks
Ali
Hi Ali,
It’s hard to tell exactly what you ran without seeing the lmer statement, but nothing stands out as problematic. The general approach sound good.
Hi Karen,
Very helpful article! I also have a repeated measures question. For my master’s Thesis I have conducted an experiment with a 2 x 3 between-within design. The between-subjects factor is in my case the advertisement type (i.e., narrative vs non-narrative structure). The within-subjects factor is the ad message (i.e., ad for brand no. 1, ad for brand no. 2, ad for brand no. 3).
Each participant was randomly assigned to one of the two conditions of the between-factor (narrative vs. non-narrative). Subsequently, each respondent viewed the three different advertisements and after each ad they had to report different dependent variables.
My Research design is balanced, I also have equal Group sizes (n=97 respondents for each group) and no missing values.
Which approach would you recommend: repeated measures ANOVAS or the multilevel approach?
Thank you very much for your reply!
Alexa
I don’t know why you say you cannot do post-hoc tests on the repeated measures factor using the multivariate approach to repeated measures. I was told I could do dependent t-tests on the repeated measure as the post hoc test using a Dunn-Bonferroni correction. Wouldn’t that work?
Hi Larry,
I suppose you could do that, but the t-tests aren’t taking into account the other variables in the model. It’s a bit of an ad-hoc approach that works, yes, but isn’t ideal.
Now, if you’re doing a one-way model with only one within-subjects effect, that would be just fine.
Hi Karen,
Thanks for this explanation, its really useful. I am still having trouble with my own dataset though and wondered if you could point me in the right direction.
I have data for 5 continuous independent variables for 22 individuals which have been tested three times each. I also have a time-varying continuous co-variate. My aim is to determine whether these variables differ significantly within- and between-individuals (and whether the co-variate has any influence).
From what I can gather from my extensive, but not very fruitful, research (I’m actually more confused now…), I will need to use a mixed model in order to take into account the repeated measures and time-varying covariate. However, rather than simply taking the repeated measures (i.e. correlated observations) into account, I would like to actually determine whether there are significant differences between trials.
Can I determine both within- and between-individual differences in these variables in the same model? I’ve been trying to use SPSS and R but am finding it difficult to know which variables to put where, or even whether this is appropriate. Any help would be appreciated.
Thanks!
Hi Carly,
Yes, you need a mixed model and you can test whether there are significant differences between trials. There is a lot to this–much more than I could do in this format. My Analyzing Repeated Measures Data covers this exactly and it’s 16 hours long because that’s how long it takes to really break down the material to an understandable level. 🙂 Here’s the link if you want to learn more: http://theanalysisinstitute.com/repeated-measures/
In the meantime, I would suggest the following free webinar recording–this is the basis of mixed models:
https://www.theanalysisfactor.com/random-intercept-and-random-slope-models-webinar/
Hello Karen. Your blog is so helpful, I appreciate it. My problem has to do with the output for the MIXED command. The output includes a table (“Type III Tests of Fixed Effects”) with columns labeled Numerator df, Denominator df, F and Sig. The ANOVA table that my mentor wants to see is the type that includes rows for each of the factors as well as the Error term, and columns for Sum of Squares, degrees of freedom, Mean Square, F and Sig value.
Is there a way that I could legitimately “convert” the ANOVA results to the more conventional format? If not, how would you recommend I report the results shown in the Type III Tests of Fixed Effects table?
George
Hi George,
Nope, there is no way. This is the ANOVA table. Mixed models just don’t use SS, so none of that is in the output.
I would just report the Fs with df and p-values.
Hi Karen,
I am currently working on my phd. Thesis and I to run a mixed model analysis. I am having trouble finding the best model that fits the data.
My project includes applying a speech perception test on children using hearing devices. The test was applied on the same group of children 3 tes over a period of 18 months. The number of subjects in each test interval is not equal which is why I need to do a mixed model analysis.
The dependent factor is: test score
There are two levels of difficulty for the test: easy and hard, all of which were applied on all children.
The repeated factor is: session time and I think
The covariate factors would be: age at receiving the device and duration of using the device.
The random factor is: subjects.
I would appreciate it if you could advise me as to what type of covariance I should use for the repeated and random factors when using spss and how to decide which models fits best my analysis.
Thank you.
Best wishes,
Nada
Oh, and I would add the time*group interaction term, to address the research question (i.e. whether there is a difference in change in the outcome variable between groups).
Hello, Karen:
I appreciate your blog a great deal.
I’m wondering about the following analysis:
I have data from an intervention study we carried out (antioxidant vs. control); outcome variables are physical function-based; for this question, let’s use ‘reaction time’ as the outcome variable. There were only 2 observations (pre- and post-6-week treatment).
I had initially done an analysis in Stata using ANCOVA, with one of the covariates set as ‘pre-intervention reaction time’ to account for inherent differences between subjects in reaction time. However, after reading another post on your site re. ‘Nancy’s’ project with similar data, I am reconsidering running my analyses as repeated measures ANOVA, given that I’m most interested in whether the mean change in the oucome variable differs between the 2 groups.
What I’m not sure about then is what I should then have as the repeated measures (I haven’t run repeated measures analyses in a while).
In stata, the command I currently have is ‘anova reaction_time ID time, repeated (group time)
For the above command, then, ID (for the individual participant), time (a dummy, categorical variable in this case for pre- and post-), and group (blueberry or control) are included.
Would you agree with this command, or would you recommend something else (e.g. using GLM). There are no missing values.
Thanks for any help!
Matthew
P.S. I may be able to run this in SPSS as well (I am having licensing issues off campus now, though).
The Blog is very useful which helped me to get clarify several concepts thanks a lot for that
Hi Karen,
My results showed a significant four-way interaction (time *three continuous variables) effect. One IV is a between subject and the other two IVs are time-varying. But I am not sure how to dig deeper into the interaction effects. Can you provide some guidance? Thank you in advance.
Hi Karen,
Thank you for this very informative article. I also have a repeated measures question. I am not sure how to approach the statistical analysis of the following study. Any insights would be greatly appreciated.
So, I have two independent groups, group A and group B. I am collecting data for 3 different tasks (Task 1, Task 2, Task 3) at 3 different time points, Pre, During and Post. There are 3 trials for each of the tasks, so I have 9 observations per subject per task (3 pre, 3 during and 3 post per task), 27 observations in total per subject. The problem is that the dependent variable, which is Pattern P, is nominal (each pattern coded with numbers from 0-5).
Group A
Task 1: Pre1, Pre2, Pre3, During1, During2, During3, Post1, Post2, Post3
Task2: Pre1, Pre2, Pre3, During1, During2, During3, Post1, Post2, Post3
Task 3: Pre1, Pre2, Pre3, During1, During2, During3, Post1, Post2, Post3
Group B
Task 1: Pre1, Pre2, Pre3, During1, During2, During3, Post1, Post2, Post3
Task2: Pre1, Pre2, Pre3, During1, During2, During3, Post1, Post2, Post3
Task 3: Pre1, Pre2, Pre3, During1, During2, During3, Post1, Post2, Post3
I am interested in pattern differences between the 3 time conditions, between the 3 different tasks and between the 2 groups. I would normally do a repeated measures MANOVA in this case, with 2 factors (Task with 3 levels and Time with 3 levels) Within-Subjects and SubjectGroup as a Between-Subjects factor, but in this case I have 3 observations and not 1. Since the measure is nominal, I can’t take the mean of the 3 trials. Perhaps, treating each trial as nested would solve the problem? If yes, can I do this with repeated measures in SPSS? Or another type of analysis would be preferable since the data are nominal? Any suggestions?
Many thanks!
I am doing MANOVA. I have a within-subject factor “fatigue”. One variable is fatigue (baseline, fatigue, rest). One of the dependent variables is the amplitude of swallowing muscle activity (T_tot_d when baseline, when subjects are fatigued, _tot_d after subjects rested). The only factor I have is Fatigue, which is the same as Time. Since there is only 1 factor and each interaction takes at least 2 factors, there cannot be any interactions in this analysis. So it is not possible to do profile plots? I don’t have a between-subject factor. How Can I do posthoc test for a within-subject factor?
Hi Karen,
I’m studying the effects of coffee intake on glucose metabolism.
I have 14 subjects, 5 treatments and 27 blood collections in each treatment.
Total of 1,890 minus the missing data (44) = 1,846.
What is the best approach – ANOVA RM or Linear mixed model (REML) ?
What is the best post-hoc test to compare the treatments?
What do you suggest me?
Kind regards,
Dear Karen,
I am having quite some trouble with finding the proper way to analyse my data.
For the study I am interested in whether a specific laboratory parameter influences the odds of obtaining a specific outcome.
In short we measured this parameter once pre-operatively, several times intra-operatively (the number of measurements depending on the length and complications during the operation, so different for all individuals) and at ICU admission.
Afterwards we measured whether patients became ‘ill’ on the first five postoperative days (y/n).
I would like to find out a couple of things.
– did patients who became ‘ill’ during any of the days have a on average lower lab-value.
– did patients who became ill have bigger changes/shifts in this value?
– is a longer time under a specific value associated with the development of this condition?
I know these are quite different questions but are clinically very relevant. For a long while I have been trying to figure out how to perform these different analysis but I am apparently not able to figure it out.
Your help is very much appreciated.
Many thanks
Hello Karen,
I am from India. One of my doctoral student has used repeated measures design to assess the effectiveness of a religious discourse of one month duration on certain personality variables, that include a measure of psychiatric symptoms. Five different tests have been made use of. Each of them have sub-scales ranging from 2 to 12. Taken together the sub-scales add up to 27, each of which can be considered as a dependent variable. Our problem is how to deal with this huge set of dvs. Can we enter each test sub-scales (dvs) one at a time? By this are we losing some information? Does that violate the rationale of a multivariate analysis? Also, can we use the mixed model you have suggested? please send a mail to the above address. Thanks.
Hi Karen,
I have some difficulties with the analysis I have to perform for my thesis. I have one independent variable (dichotomous), one moderator (dichotomous) and a dependent variable dichotomous, for the second analysis the DV is continuous. I have a lot of repeated measures, so I have to deal with between as well as within subjects. The suggested analysis was Random coefficient model, but now I am not sure how to perform this (I am using Stata for the first time). I have a long form dataset like below:
Id Id_product IV MOD GEN Y1 Y2 INT_IV*MOD
1 1 0 0 Male 0 0
1 2 0 0 Male 1 1
1 3 0 0 Male 0 2
1 4 0 0 Male 0 0
1 5 1 0 Male 1 0
1 6 1 0 Male 0 0
1 etc
2 1 0 1 Female 1 0
2 2 0 1 Female 1 0
2 3 0 1 Female 1 3
2 4 0 1 Female 0 1
2 5 1 1 Female 0 1
2 6 1 1 Female 0 0
2 etc
Is the random coefficient model the correct model to use? Or is there another/better analysis? Thank you in advance.
Hi Daphne,
Yes, you’re going to need some sort of random coefficient or repeated measures model. Which to use depends on a lot of details.
These are complicated models, so I would strongly urge you to get some stat consulting if you’re new to stats. It’s not beginner-level stats.
Hi Karen,
I am running a Mixed Model analysis in SPSS. The dataset contains two Fixed factors let’s say A (two levels) and B (three levels). There is a significant interaction, and with the EMMEANS command I’ll be able to follow that one up. I would like to report t-statistics on the post-hoc testing. The output shows me, however, the mean differences (with associated p-values etc.). Did I do something wrong, or is there another, better, command? In sum my question is, how to get post-hoc t-statistics from a Linear Mixed Model procedure in SPSS? Thanks so much in advance.
Desiree
Hi Desiree,
The only way to do it is through EMMeans. If you’re trying to do it on the interaction, you have to use syntax. There’s no option in the menu dialogs. Use a compare statement with a post hoc adjustment.
Thank you very much, Karen.
Desiree
Hi,Karen. I have a 2-level data set with 50 measurements (level 1) nested within 62 subjects (level 2).
Some brief context: the subjects were randomly assigned to one of two training conditions. After training, all subjects rated the same 50 essays.
The level-1 measurements are binary: they take a value of 0 for “inaccurate” and 1 for “accurate.” Accuracy denotes that the subject’s score matched the resolved expert score.
Training condition is my level-2 covariate.
It seems reasonable to fit a GLMM to the data given the clustering of measurements within subjects and that the outcome is binary. What I’d appreciate is some guidance on appropriately specifying the repeated measures aspect of the design. All subjects scored the 50 essays consecutively, so time is really not in play. If I use the HLM software, are there particular settings I should modify, other than changing the outcome type under “basic settings”? Or would you recommend the GLIMMEX procedure instead, using SAS?
Many thanks!
Hi Kevin,
While I have HLM software and have used it (and it will probably work just fine for what you’re doing), I don’t know it as well as SAS. So I would recommend SAS proc glimmix (or even genmod for a GEE model), but that’s my own bias.
Thanks, Karen!
Dear Karen,
I am just starting out using spss. we have completed an in class music study for which between subjects design mann whitney u is appropriate and likert cale scoring. there is a happy music change score and a sad music change score in the data provided and i need to get descriptive statistics and inferentials.
Firstly I am confused as to what info to transfer in which box. The inferentials has a test variable list and a grouping variable list. While im aware that the independent variable is the music order and the dependent variable is the mood score, the info represents as happy music change score and sad music change score and i’m not sure what goes in the dependent list.
secondly for inferentials i have a test variable list and a grouping variable list. My variable are gender/age/happy music change score/sad music change score. with 16 participants to include only three males.
Lastly its an in class experiment to facilitate the writing of a lab report, but i’m really in need of some guidance with spss.
can you help with this?
Rachel
Hi,
Need help for statistical design.
I am trying to build a table for statistical significance of my EEG analysis data.
I need to compare 50 different Hz for each animal with repeated measures (3 EEG recording sessions) between at least 3 groups (non-treated; treated with drug; treated with vehicle).
I came up with ANOVA with repeated measures. My problem is that I will have 50 data points/animal. Thank you for your suggestions.
Angelique
Hi Angelique,
You really have two repeats–one across conditions (Hz values) and one across time. So really, you have 150 data points/animal, right?
There are a few different ways to approach it. You could do a RM ANOVA, although I suspect that will get messy fast. Otherwise, you really need a mixed model.
This is not a simple example of a mixed model, and it’s hard for me to explain much more without understanding where you are in understanding. Have you ever done a mixed model?
Karen
Hello Karen,
I am working on my data analysis for my thesis in psychology and I am using spss. My data was previously collected on 2 NASA NEEMO missions. I have 12 subjects (6 subjects from each mission). I have 2 time points (1st & 2nd half mission). My IV is sleep restriction (2 measures: total sleep in hrs/by Actiwatch -with one value for each day and quality of sleep/by sleep log – with one value for each day) and my DVs: are Mood (POMS – 6 subscales and 1 scale: total mood disturbance which is calculated from the 6 subscales, POMS was taken 2x for the entire mission; once during 1st half of the mission and once during 2nd half of mission) and Cognitive performance (PVT/reaction time in milliseconds, has multiple values for each day). H1: sleep restriction will have a negative effect on an individuals mood. H2: sleep restriction will have a negative effect on an individual’s cognitive performance. I am missing pvt/reaction time values for a couple of subjects during the 1st half of the mission. I am having difficulty identifying how to set up my data in spss – I believe it should be mixed model – linear, but after that – i’m not clear on how to proceed. Thank you in advance for any direction you can provide me regarding how to proceed. thank you, Pam
Hi Pam,
These designs can get complicated fast. The basic idea is that you want to set up the data so that each time you observed the DV for an individual, it’s on a separate row.
The tricky thing here is sometimes knowing how to define the DV (it sounds like it should be obvious, but it’s not). So for example, you have mulitple reaction times per day per person per time period. Those should each be on one row. But are the 6 mood subscales 6 different DVs or 6 observations on one DV?
I’d need a lot more detail to really be helpful. I’d recommend a consultation if you need help right away. 🙂
Hi Karen,
I am working on an analysis that measured salivary cortisol and serum cytokines at two times during pregnancy in the same women and am interested if the interaction between cortisol/cytokines predict maternal depressive symptoms on a survey. As all of my variables are continuous I am unsure how to precede as I cannot perform a traditional RM ANOVA. Any guidance you can provide would be great. Thanks!
To recap:
IVs: cortisol and cyotkine interaction score (continuous collected on same women twice during pregnancy)
DV: maternal depression score
Hi Kimberly,
You would probably want a marginal model–with only two time points, it gives you more flexibility than mixed.
The key is putting it into Long Format. Here’s more info on it: https://www.theanalysisfactor.com/wide-and-long-data/
Every software package has a way of doing the switch, so don’t try to do it by hand. You’re more likely to make mistakes. 🙂
Hi Karen,
I am running a repeated measurement longitudinal analysis of whether interactions between cortisol slope and serum cytokine measurements measured multiple times during pregnancy (early and mid) predict depressive symptoms. As all my variables are continuous I am unsure how to precede since I can’t perform a traditional RM ANOVA. To recap this is what I have:
IVs: cort/cytokine interaction at time 1 (continuous) and cort/cytokine interaction at time2 (measured at times 1 and 2 in same subjects)
DV: maternal depressive symptom continuous score from a survey
Any help you can provide on how to precede would be very helpful. Thank you!
Kimberly
Hi
for my thesis work at each month (may june and july) when i anaylse soil pH plough had significantly (p<0.05) lower soil pH than minimum tilage. But when i ran it through repeated measurements i get tillage treatments to be significnat, time significant but tillage x time interaction non- significant. Can it be like this? what does it implies to me
Yes, that can happen and it’s quite common. It means that the change over time is the same for both tillage groups.
Hi,
I am doing a study on microgeographic variation in bird song complexity in a particular bird species, using 8 parameters (such as syllable diversity and Shannon entropy) to measure complexity.
More specifically, there are two separate areas within one big study site, one area has high levels of habitat complexity and quality (forest), the other is of low habitat complexity (open fields). I am comparing the song complexity of the population between areas with the hypothesis being the birds inhabiting the better quality habitat will have the more complex songs (preliminary data supports this).
I have data from 9 individuals from each of these 2 areas (n = 18 in total). I have recorded the songs of these 18 individuals and analysed their songs in order to extract data for the above-mentioned song parameters. Now, my query is I have obviously recorded and analysed multiple songs from each individual. So I was wondering what statistical analysis test you recommend I should use? I have analysed 417 songs in total: 166 from area 1 and 251 songs from area 2. Nine individuals per area were analysed.
I hope this makes sense!
Many thanks and best wishes
Sam
Hi Sam,
It sounds like you’ll need some sort of mixed model. In order to actually advise beyond that, I’d need to ask you 20 questions about how you’re measuring everything and exactly what you want to compare. I think it’s pretty straightforward, but of course, the devil is in the details. 🙂
Hi Karen,
I’m currently unsure of the statistical tests I need to run for my data. I’m running a 2-species plant competition experiment, and there’s a total of 15 densities in total.
Height data is collected for each plant on a fortnightly basis, and I’ve in total 10 weeks worth of data. What test can I run to determine the effect of one species on the other? and whether the result is statistically significant?
Thanks in advance!
Leo
Hi Leo,
It sounds like you could run any of the models outlined in this article, but of course, the trick is to decide which one and how exactly to specify it.
Much would depend on the exact design. For example, you say it’s a competition study. Are there two plants, one of each species, in each pot? More than one of each?
Are they on different plots of land and we need to control for the sunlight, temperature, soil quality?
In other words, it’s all in the details, so you’d need to give me a lot more information. I’m happy to answer questions, but don’t like advising on an analysis without talking with someone. There are too many details I need to ask about.
Karen
Hello Karen,
I am struggling with my syntax for a composing a repeated measures mixed model. My 168 students are divided into 3 conditions. Each student needs to write 3 abstracts and more particular, they have to write a draft and final version of each abstract. By restructuring the data, I created a variable ‘moment’, which is ( 3 abstract x 2 versions). Students receive a ‘score’ for each of the 6 moments.
At the moment my syntax looks more or less like this:
MIXED score BY Moment conditie
/CRITERIA=CIN(95) MXITER(100) MXSTEP(10) SCORING(1) SINGULAR(0.000000000001) HCONVERGE(0, ABSOLUTE) LCONVERGE(0, ABSOLUTE) PCONVERGE(0.000001, ABSOLUTE)
/FIXED=Moment*conditie | SSTYPE(3)
/METHOD=REML
/PRINT=R SOLUTION TESTCOV
/REPEATED=Moment | SUBJECT(ID) COVTYPE(UN).
GRAPH
/LINE(MULTIPLE)=MEAN(score) BY Moment BY conditie.
My graph looks ok, but my model appears not to fit…
How can I adapt my syntax, so it just shows the difference in scores between the three conditions? It doesn’t seem that difficult, but I already lost loads of time.
Thanks in advance
Mario
Hi Mario,
A few things:
1. It just might be that there just isn’t a meaningful difference between the three conditions. So remember that’s a possible option.
Ah, do you mean you just need a printout of what the difference IS? You need an EMMeans statement. /EMMEANS=TABLES(Conditie) COMPARE
2. Your syntax looks good and your analysis seems to be reflecting the design. The only thing is you may want to check whether an unstructured covariance structure is necessary. It’s using up a lot of df to calculate that many parameters.
Karen:
I think my question is simple, but I am really struggling with it. I have kids who completed summer programs that were one of three levels: Math, Science, or combination. We pre and post tested them on a normed math test.
I want to run a repeated measures but the size of the groups is nowhere near equal (Math = 320, Science = 41, Combination = 37). When I run a GLM repeated measures I show a significant interaction, but don’t really trust the results due to the differences in group size. How can I control for this and determine the degree of interaction between these groups? Looking for answers has left me more confused than enlightened to this point.
Thank you in advance for your insight.
Jeff
Hi Jeff,
You’re right to trust your instincts. Interactions can be affected by unequal sample sizes in any type of ANOVA. Pay careful attention to the patterns of means and mean differences to see if the interaction makes sense.
Dear Karen,
I hope u can help me to sort out my questions. because i really get confuse to use which statistical analysis for study design.
Its a randomized placebo trial with equal sample size; treatment vs placebo. and i want to measure the changes of treatment
1. treatment vs placebo at different weeks (baseline, 4th weeks, 8th weeks and post treatment)- between groups
2. treatment effect at different weeks in each group – within the group
so which is the best analysis to use in spss?
Hope u can help me with this
Thank you
Hi Ramlah,
This is one that could be done a number of different ways, and figuring out which is best would require fitting some data.
That said, I would start by graphing, then try both a mixed and a marginal model and see which fits best. I suspect either would work well.
Dear Karen,
I think you are the right person to help me in sorting out an interpretation of JMP reports. I have a random effect and 2 fixed effects in my analysis. I am applying a mixed model to test the effects of both terms on my dependent variables. I need to know the percentage of variation explained by the fixed and random effects. Do you know where I can read these outcomes in the reports of JMP? Is the R2 the variation explained by the fixed effects? I am fitting my model with REML algorithm, therefore the report I get in JMP is:
REML Variance Component Estimates where I can read the Variance Component, Standard Error, Pct of Total for random effect and residual. What does the residual represent?
Thanks a lot
Hi Francesca, there isn’t a way to get R-squared in a random effects model with REML. There is ICC, and you can see how the different variance components change as you add predictors.
“What does the residual represent” is a question that would take me a long time to answer in any useful way. I would suggest you watch my “Random Intercept and Random Slopes Models” webinar. It’s free and you can dlownload the recording. https://www.theanalysisfactor.com/random-intercept-and-random-slope-models-webinar/
Better yet, we go into massive detail about this in my Repeated Measures Workshop. http://theanalysisinstitute.com/repeated-measures/
Hi Karen,
Your website is extremely helpful and it’s so nice of you to answer people’s specific questions! Perhaps you can help me.
I am running a cross-national analysis of the number of violent incidents in each country from 1998-2007. The data is stacked such that I have 10 lines for each country. Each line having the DV, the number of incidents in that year, and a number of IVs measured for each country that change for some countries over time and not for others (population size, measures of diversity, democracy/freedom scale, GDP, etc). The data is longitudinal and clustered regionally (Europe, Middle East, etc), so I have been using HLM (repeated measures w/in individuals –with the Poisson distribution because the DV is a count variable and is often 0 and skewed to the right). I include the annual measures at level 1 and the regional variables at level 2. Unfortunately, I have run the analysis multiple times sometimes including/excluding certain variables and the results do not seem to be robust (despite focusing on the unit-specific model with robust standard errors). As a result, I am looking into other ways that may be more appropriate to analyze the data. Would you recommend the linear mixed model because it adds additional random effects, like HLM does? I’d really appreciate your advice!
Thanks!
HI KB, it’s hard for me to recommend an analysis without asking many detailed questions, especially with that level of complication.
That said, if it’s Poisson distributed, you don’t want to use a linear mixed model. You have to account for the Poisson distribution. I assume by HLM, you mean the actual software. What you’re using sounds reasonable, and it’s pretty common in any model for results to change depending on the predictors included.
Hi Karen, this is extremely useful. If I understand correctly, Method 2 is similar to Method 3, except no random effects are modeled. Am I correct? e.g., if you were to call spss’s MIXED and specify nothing at all as random, you’d be adopting Method 2, even if you are using REML and selecting a variance-covariance matrix to be modeled. Is this right?
Do you have some advice for general texts/citations to consult for more information on Method 2?
Thanks!
Hi Kim,
If you were to call spss’s mixed AND include a Repeated Statement instead of a Random statement, then you’d have Method 2. Yes, you are still selecting a covariance structure, but it’s on a different matrix than if you used a Random statement. Which covariance matrix you’re modeling is the crux of the difference.
If you have neither Random or Repeated, it defaults to a linear model.
Dear Karen,
I’m somehow stuck with the statistics of my study design. I have two groups of experts with unequal group sizes (between-subject factor: expertise, 25 non-experts vs. 30 experts). For each test person I measured reaction times at 5 different stimulus durations (within-subject factor: stimulus duration, 4 levels). My approach was a 2-factorial ANOVA with an unbalanced design (due to the unequal group sizes).
Now my question is, if this is a marginal multilevel approach, and if I have to control for the repeated measurements, since they are already in the within-subject factor?
If I have to control for the repeated measures, is it ok to include the test person as a random, (in expertise) nested factor?
Thanks a lot, for your help…
Greetings, David
Now
Hi David,
See my response to Hayley about giving advice without all the details.
So you have a 2×5 design, with expertise between subjects and duration within.
The marginal model will account for the fact that the duration is within subjects (aka repeated). You’ll define duration as the repeated factor and subject ID as the subject.
The other approach would indeed be to make Subject (nested within expertise) as a random factor. Depending on the covariance structures you choose, you could even get identical results in the two approaches.
This is exactly the kind of stuff we cover in my Analyzing Repeated Measures workshop. We’re offering it again in the fall, but if you can’t wait until then, I would recommend a Quick Question consultation. We could seriously get this figured out within an hour, and I promise you’ll understand it. 🙂
Can you help me see which approach I should use?
I’m doing an education study and I’m trying to see the effect of website usage on quiz scores in a college plant identification class. There were 30 students in the class and they took 10 weekly quizzes over the course of the semester. They also had a website where they could log in and use a study tool. The website kept track of the time they were online.
So my dependent variable is quiz score (continuous) and my predictor variable is website usage over the previous seven days (also continuous).
What I essentially want is a scatterplot with a regression line, showing whether using the website improved the quiz score. But to get there I need to control for differences between the students and differences between the quizzes. Each student took 10 repeated measures, and those 10 measurements were slightly different from week to week. So if I’m looking at my data set in the wide format, I need to control for differences between the rows and differences between the columns.
I tried using “General Linear Model > Repeated Measures” in SPSS, but I can’t figure out how to tell the program that website usage is a single, continuous predictor variable. And I also can’t figure out how to control for the shifting class average from week to week. Can you give me any guidance?
Thanks!
Hi Gareth. What you’ve got is a time-varying covariate: website usage each week.
The bad news is that repeated measures ANOVA can’t incorporate time-varying covariates, but the good news is that mixed models can. With both repeats over students and repeats over quizzes, you have a classic example of a crossed random effects model. Here’s something I wrote about it: https://www.theanalysisfactor.com/multilevel-models-with-crossed-random-effects/.
These can be tricky, so depending on your stat background, you may want to read more–Snijders and Bosker’s Multilevel Analysis book has a chapter on it, but it’s somewhat mathematical. If that is too big of a jump for you, I would honestly suggest a consultation. It’s something we could sort out in an hour, most likely.
Karen
Thank you Karen, I will do what you proposed. And thanks for everything you are doing to help us!
Hi karen,
I am doing a GLM repeated measures analysis with levels of burnout measured at Pre and Post. I also have 5 categorical IV’s (2 of them with 2 categories and the other 3 with 3 categories). If I put all of them in the model and just ask for a design with 2-way interactions (time*each of the IV’s), I see a significant increase of Burnout for one category of one of my IV (level od education). However, if I run the same model but this time including 3-way interactions (time*IV*IV) in the design, the significant increase observed for one category of level of education (in the 2-way interactions) is now not significant. In fact, there is now a significant DECREASE for the other 2 categories of that variable. Does it make sense? Why is that including 3-way interactions in the model changes all the results for the 2-way interactions? Is it because I have too many variables/interactions in my model? Should I just look at my model including the 3-Way interactions instead of doing it step-by-step. Thank you so much. JF
Hi JF,
It’s hard to tell without a thorough examination of the output what is going on.
It’s possible that there really are 3-way interactions, but when you don’t include them in the model, their effects are getting “pushed” into the 2-ways.
I would suggest doing a bunch of graphing. Plot the EMmeans across the 3 way interactions, then the two-way. See where the differences in means are the same across time and where they aren’t. You could also do this through investigation of means from a table, but I personally find it much easier to see if I plot them.
Karen
Sir, please tell me the statistical technique by which I can compare the multiple measurements of multiple treatments. Like many recovery measures of blood pH of different exercises.
Hi Pardeep,
I would need a lot more information to answer that. I can interpret it a few different ways.
Karen
Hi Karen,
I am trying to use repeated measures anova for plant varietal treatments that were sampled across time. It is ok to use it for plant populations instead of individual plants? Second, I am using JMP software, how can I approach the post-hoc test? thanks,
Paola
It can be okay if the plant populations are the unit of measurement. I’d had to see it to be sure.
And I haven’t used JMP in a while, so don’t know the post hoc tests off the top of my head. If anyone else knows, please feel free to comment. Karen
HI KAREN
frst of thank you very much for clarification of my statistical confusions on the area of mixed model analysis for repeated measures. I get the website very useful for researchers. we need more explanation with statistical software like SPSS and STATA
Thank u
Demewoz Haile
Hi Demewoz–You’re welcome. Glad you found it helpful.
Karen
Hi Karen
I really need your help. I am working in child welfare and have the following variables to analyze:
-repeated administrations of a tool (strengths and needs which as questions on social support, income, drug use etc).
-whether they are an adult/child
-where they are now (child in care, at home etc)
what I am really interested in is in seeing whether our involvement (the intervention) had any effect on strengths and needs. I anticipate that the strengths will go and the needs will go down over time (over our intervention). However, I am unsure as to how to analyze this data. Originally I thought about a repeated measures ANOVA but I am not happy about the fact that you need complete data or it will boot out the cases. Inputting missing data is not feasible as my data is ordinal. I thought about regression but do I have to use polytomous?
Any advice will really help,
Gissele.
HI Gissele,
It’s hard to tell you how to proceed without all the details, but if you have missing data in the response variable, you’re right, repeated measures ANOVA won’t work. Actually, even without the repeat, if the outcome is ordinal, no ANOVA will work.
You probably need a mixed model, and since it’s ordinal, a Generalized Linear Mixed Model. Here are two resources that might help parts of this. If you want help putting it all together, I can only suggest a Quick Question consultation so that we get all the details straight.
This webinar recording is an example of testing effects over time: Random Intercept and Random Slope Models
And this article discusses GLMM: Five Extensions of the General Linear Model
Hi Gabriela,
That should work pretty well. Usually the tricky part is post-hoc tests for the within-subjects factors.
Which software are you using? I can tell you better how to approach it.
Karen
Hi Karen,
could you write a bit more about post hoc tests in mixed models? in my research I have repeated measure and 2 between subject variables on two levels (for exaple sex and age [young and old]. I have difficulities in running post hoc for interaction of between subject variables, could you give me a tip how to deal with it?
Thanks for any advice!
Thanks, Karen!!
Hi Karen,
Love your site! I was just wondering if you could expand a little on your explanation for approach 1 (GLM) and post-hocs. In particular, what should you do if you have a significant interaction between your RM factor and one/more between-subjects factors? Is it OK to run ANOVAs/ANCOVAs at each level of the RM factor, or is the error term not appropriate?
(To put this slightly rambling question in context, I am using RM ANOVA/ANCOVA with brain imaging data. I have a region of interest, ROI, and because I have measured ROI’s volume in the left and right hemispheres, my within-subjects factor has those 2 levels. I want to look at asymmetry effects, and also effects of clinical group and gender (and their interactions), and also build a second model that includes whole brain volume as a continuous covariate/control variable.) Thankyou so much for any advice you have!!
Hi Ali,
Those are tricky. In a between subjects model, you would run simple effects and change the error term (Keppel’s Design & Analysis has a nice chapter on this). But there are multiple error terms in a repeated measures GLM.
I would personally rerun it as a marginal model in mixed software, and use the multiple comparisons options in the EMMeans (SPSS) or LSMeans (SAS) statement. You have a pretty straightforward model.
Karen
my research question is to examine the effects of odors on consumer behavior and the moderating effects of sex and need for stimulation on the relationship between odor and consumer behavior. My variables are:
1 – Independent variable: odors (three experimental conditions: the presence of odor x, y presence of odor, no odor)
2 – Dependent variable (continuous variables): reactions of consumers
3 – moderating variables: need for stimulation (continuous variable: a number of Likert scale items) and Sex (Categorical variable)
My question: how to test in spss moderating effects of need for stimulation (the measurement scale of this variable has several items? Can we recode into two categories (high vs. low need for stimulation need stimulation) by considering that the respondents less than 4 on a Likert scale to 7 degrees with a low need for stimulation and those who responded more than 4 have a high degree)? What is the exact procedure to do in SPSS?
Thank you
Hi Karim,
I’m assuming all your variables are between subjects b/c you didn’t say otherwise.
A moderating effect is just an interaction. So put in an interaction term between Odor and Need for Stimulation to test that moderation. You can do this regardless of whether the moderator is continuous or categorical. It doesn’t matter. You do need to interpret them differently b/c you have to use the regression coefficients. If you’re not familiar with interpreting interactions in regression, I would recommend watching this webinar recording. Interpreting Linear Regression Parameters: A Walk Through Output It’s free.
You have to be careful about categorizing continuous predictors. It CAN make sense, but usually you just lose information.
Thank you for your clarification. As a matter of fact, I’m struggling with this material since I’m looking for an appropriate method to analyze my thesis data.
Could someone here maybe help me out a bit? I have a relatively simple design, yet the analysis is somewhat complicated. I have a 2×2 between subjects design in which I measure measuring product evaluation. So far, nothing complicated. But, one of my between-subject factors has 4 different replications, resulting in 16 different experimental conditions.
Moreover, I’m also using 4 (within-subject) replications (different product categories), resulting in an unbalanced mixed-design. I understand that the latter fact rules out Repeated Measures ANOVA as an option. Someone suggested using Linear Regression, but unless I used some kind of Repeated Measures Regression, I will violate some assumptions.
Any suggestions?
Hi Elvin,
First, I apologize for the late response. I was out of town with very haphazard internet access (and I’m only now getting over the withdrawal symptoms).
Yes, you’re going to need to run a mixed model. You have a variation on a randomized block design. Most Design of Experiments text books have chapters on these models.
You’re right that the repeated measures anova won’t work if it’s unbalanced. You are going to need to run a mixed model. If you want some background info (it won’t answer all your questions or give you step-by-step instructions on how to run it, but it will give you a framework in which to approach it), I would recommend my webinar Fixed and Random Factors in Mixed Models. It’s free.